1. Introduction
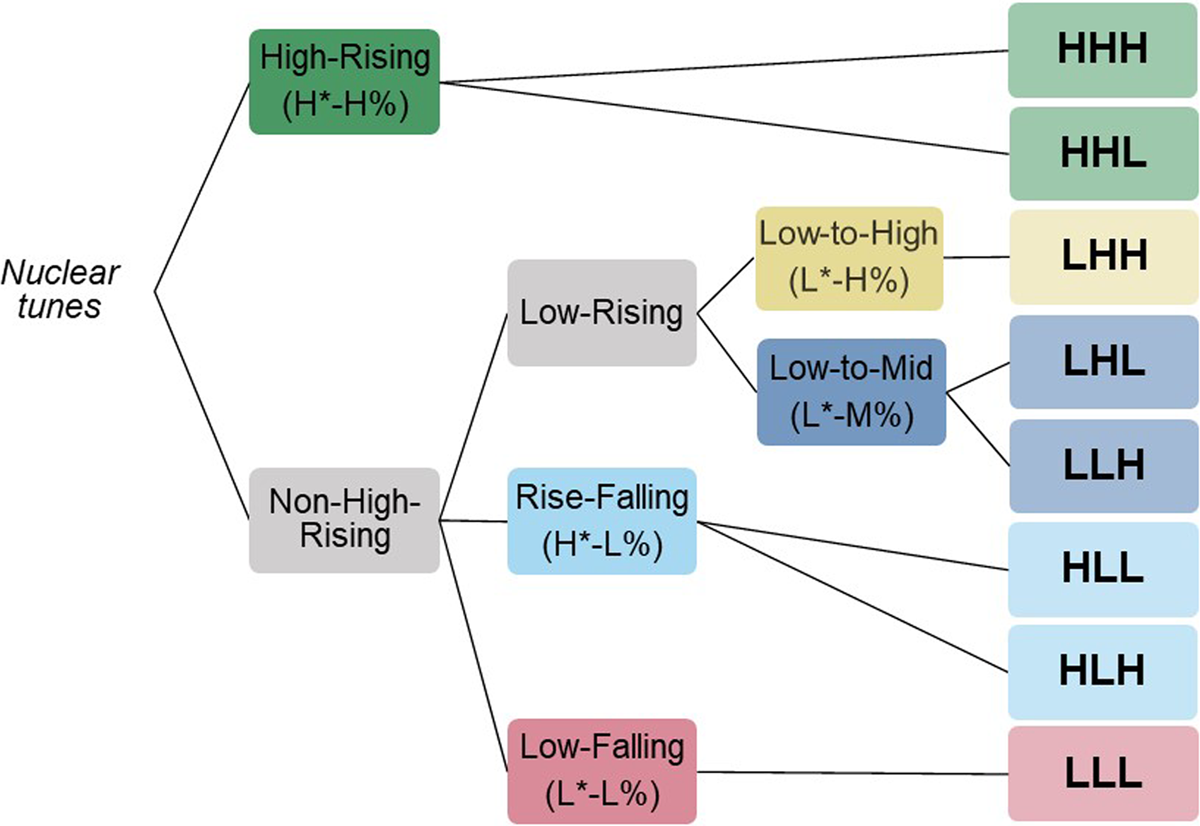
In American English (AE) intonation, the pitch pattern in the final region of a prosodic phrase conveys pragmatic meaning. The phonological analysis of the system proposed in Pierrehumbert (1980; see also Ladd, 2008), couched in the theory of Autosegmental-Metrical Phonology, analyzes the phrase-final pitch pattern as defined by the concatenation of three (phonological) components: The pitch accent, phrase accent, and boundary tone. These components are specified in terms of the tonal primitives H(igh) and L(ow), which determine relative pitch targets for the syllables to which they associate. The sequence of phrase-final pitch accent, phrase accent, and boundary tone is referred to as the ‘nuclear tune’, based on the status of the pitch accent as marking the obligatory phrase-level (so-called “nuclear”) stress. In phonological approaches, the pitch patterns generated from the tonal specification of a nuclear tune are implemented with interpolative pitch movements between successive tonal targets, yielding a dynamic pitch pattern that extends from the location of the nuclear stressed syllable to the end of the phrase. Considering only the monotonal pitch accents (i.e., setting aside the downstepped high tone (!H) and bitonal pitch accents (L+H*, L*+H, H+!H*) proposed for AE intonation1), and the proposed inventory of phrase accents (L-, H-) and boundary tones (L%, H%), this system generates a set of eight (2 × 2 × 2) tonally distinct nuclear tunes, which map onto eight distinct pitch trajectories that are (in principle) available for encoding pragmatic meaning contrasts. We refer to these eight as the set of ‘basic’ nuclear tunes.
Despite the wide acceptance of this model, relatively little work has scrutinized the extent to which speakers of AE produce the full range of distinct intonational melodies predicted by the AM model. Some evidence for distinctions among discrete tune categories is found in studies on intonational meaning that show associations between particular tunes and pragmatic meaning (e.g., related to illocutionary force, speech act, or the speaker’s epistemic state). Although there are many such studies in the literature, none address the system of contrast among more than a few tunes at once. Further, many studies do not specify the phonological tones or characteristic f0 contours of the tunes they analyze. Thus, even though there is some support for the general claim that certain tunes are contrastive on the grounds that they are associated with distinctions in pragmatic meaning (e.g., Hirschberg, 2004; Prieto, 2015; Westera, Goodhue, & Gussenhoven, 2020), there is not yet solid empirical support for the claim of an eight-way phonological contrast in the basic tune inventory.
The present study aims to address this gap by examining evidence for the phonological status of the eight basic nuclear tunes as distinct categories in mental representation for which there are systematically distinct acoustic realizations. We approach this question from the dual perspectives of speech production and perception (described in detail in section 2). First, in an imitative speech production task (Cole, Tilsen, & Steffman, 2022; following Chodroff & Cole, 2019), participants listen to model utterances exemplifying one of the eight tunes, and then reproduce the melody they heard on a new sentence, in effect, transposing the melody to a new phonological base (i.e., new segmental content). Second, in an AX perceptual discrimination task, participants listen to pairs of tunes from the model utterances used in the imitation study and identify if they are the same or different. If the findings from these experiments show that all eight of the hypothesized tunes are distinctively produced and perceived by speakers of American English, the AM model would be substantiated in the claim that these tunes have discrete (phonological) representations, are adequately distinguished in their phonetic realization, and are available for conveying distinctions in pragmatic meaning. Conversely, if certain distinctions are not manifest in the production or perception data for these tunes, their status as distinct intonational categories in phonological representation would be called to question.
We follow prior studies in using an imitation task to investigate the phonological status and phonetic implementation of intonational features (e.g., specified in terms of H(igh) and L(ow) tones) (Pierrehumbert & Steele, 1989; Braun, Kochanski, Grabe, & Rosner, 2006; Dilley & Heffner, 2013; Cole & Shattuck-Hufnagel, 2011; see discussion in Gussenhoven, 2006). Alternative elicitation methods using discourse prompts are not feasible for our present purposes; existing, empirically informed work on tune meaning focuses either on a small subset of tunes or a single dimension of pragmatic meaning (e.g., Burdin & Tyler, 2018; Jeong, 2018; Nilsenová, 2006; de Marneffe & Tonhauser, 2019; Rudin, 2022), and therefore such studies are insufficient for identifying potential meaning contrasts for the entire tune inventory, or even for the set of eight basic tunes that are investigated here. A more comprehensive account of intonational meaning has been proposed by Pierrehumbert and Hirschberg (1990), but there is not yet empirical validation for the complete model to support the predicted tune-meaning associations.
Using an imitation task has the advantage that tune elicitation does not depend on an explicitly specified meaning or congruent discourse context. Rather, tune imitation involves, as a first step, an encoding of the tune presented in the auditory stimulus in terms of its phonetic properties and the associated phonological categories, and second, an implementation of that same tune in speech production. Of course, imitation from auditory models is key for language learning, but prior work shows that even in a laboratory setting, speakers are capable of imitating at least some aspects of phrasal intonation, even in the absence of an explicit discourse context (Cole & Shattuck-Hufnagel, 2011). Notably, though, not all aspects of intonation are imitated. For instance, prior work on AE finds that peak alignment is imitated but peak height and f0 velocities are not (Dilley & Heffner, 2013; Dilley, 2010; Tilsen, Burgess & Lantz, 2013). Distinguishing those properties of a tune that are reliably imitated from those that are not therefore offers a window into the mental representations involved in the transfer of information from perception to production. Finally, imitations can reveal both category structure of the stimuli and the patterns of variation around those categories. For instance, Braun et al. (2006) show that iterated imitations of randomly varying phrasal f0 patterns reveal a small number of attractor patterns that correspond roughly to proposed (phonological) intonational categories, while also exhibiting substantial phonetic variation around those attractors (Braun et al., 2006).2 To summarize, using an imitation task in intonation research avoids reliance on uncertain distinctions among tunes in their discourse function, and offers a window into the robustness of discrete tune categories and the parameters of variation within and between those categories.
The experiments proposed here use a variant of the imitation paradigm in which participants reproduce an intonation pattern from multiple sentence stimuli by mapping the abstracted pattern onto a new sentence. This method diminishes the role of information specific to the heard stimulus that is stored in the participants’ short-term memory, with the goal of tapping into the representation abstracted from the auditory stimuli and specified in terms of intonational elements that are part of long-term memory representations. We assess the f0 trajectories of imitated tunes to determine the nature and robustness of distinctions that speakers produce, using a variety of analyses. Distance analysis: Modeling f0 trajectories of imitated tunes as time-series data, we measured the difference between the imitation and the model tune for each trial in terms of the mean distance (RMSD) between paired f0 points along the two trajectories. We also examined pairwise distance (RMSD) between tunes as a measure of the separation between tune pairs in phonetic space, comparing pairwise separation of the model tunes with that of the imitated productions. Clustering analyses: Modeling f0 trajectories of imitated tunes as time-series data, we test how the f0 trajectories cluster using a bottom-up analysis that is blind to the category of tune that was the intended target of imitation on a given trial. Machine classification: The emergent clusters are compared with the classification accuracy of a neural network trained on the same imitated tune productions. Together, these analyses allow us to assess whether all eight of the basic tunes are distinguished from one another in the acoustic space of the f0 trajectories, and which tune distinctions are more (or less) robustly captured in the imitations. Analysis of fine-grained acoustic variation: We complement the results from clustering and classification analyses with more traditional modeling approaches (Generalized Additive Mixed Modeling and mixed effects modeling of temporal alignment measures) to examine the nature of distinctions among the imitated tunes, testing how tunes are realized in terms of f0 targets and turning points. These acoustic details of the imitated tunes are compared for their similarity to the auditory models (the stimuli for imitation), and to the predictions of the AM model. Individual speaker variation: All of the above analyses are conducted on data aggregated over participants. We compare the group data to results from clustering analyses of individual speakers, asking how much speakers vary in their productions and what commonalities emerge. Perceptual discrimination: Given that successful imitation depends on the accurate perception of tune distinctions, we examine the perceptual distinctiveness of the f0 trajectories of the model tunes used as stimuli in the imitation experiment to determine to what extent perceptual discriminability predicts the presence and robustness of distinctions in speech production.
Across our production and perception experiments, we are looking at measures of tune distinctness for evidence of the hypothesized categorical status of the eight basic nuclear tunes. To the extent that a specific tune is clearly distinct from others in production and perception, it is evidence supporting a representation of that tune as a discrete phonological category, distinguished from other tunes.3 Conversely, a tune that fails to be distinguished from other tunes in production and perception also fails this particular test of category status. Importantly, any pair of tunes that are not reliably distinguished in perception and production would be poor candidates to mark a corresponding distinction in pragmatic meaning, so findings from this study have implications for accounts of intonational meaning in AE. Notably, Pierrehumbert and Hirschberg (1990; hereafter PH) propose an account of AE that associates a distinct pragmatic meaning for each nuclear tune tested in the present study,4 so a failure to confirm the distinctive status of any of the tunes we test would call for a re-examination of that proposal. In this way, the findings from our study provide a partial test of the PH model for AE (as it pertains to a specific subset of nuclear tunes), and its basis in a specific inventory of tonally contrastive pitch accents, phrase accents, and boundary tones. On the other hand, tune distinctions that emerge in our data as robust in perception and production are good candidates for encoding pragmatic contrasts. By examining the f0 trajectories of tunes that are successfully distinguished by speakers and listeners, we will provide evidence about which aspects of the tunes are accessible and therefore available for encoding pragmatic meaning contrasts. The analysis of imitated tunes will also inform our understanding of how the phonological distinctions among tunes are phonetically implemented, and how tune implementation aligns with predictions from the AM model.
The paper proceeds with a discussion of experimental methods, measurements, and statistical models for both the production and perception experiments in Section 2, followed in Section 3 by results presented in the same order. Section 4 presents a detailed comparison of results across datasets and analysis methods, and a discussion of generalizations obtained across the comparison sets. To preview, the findings within and across analyses converge on a system of up to five hierarchically ordered tunes, with a primary distinction between tunes with a high-rising shape (hereafter, the High-Rising class) and other tunes (Non-High-Rising), which is robust in production and perception. A set of secondary distinctions are evidenced within the Non-High-Rising class, though they are both less robust in perception and more variable across speakers in production. Additional variation within these five tune classes aligns with predictions from the AM model, which, however, are the smallest and least robust distinctions overall.
2. Methods
This section describes the methods for two experiments. First is the imitative speech production experiment in which participants listen to several auditory models of the same tune and reproduce the intonational melody on a different sentence. Second is the AX “same/different” perceptual discrimination experiment in which participants discriminate pairs of tunes, listening to the auditory model stimuli from the speech production experiment.5 Some details in the methods are abbreviated here; however, a fully detailed methods section is available in the open access repository.
2.1. Stimuli
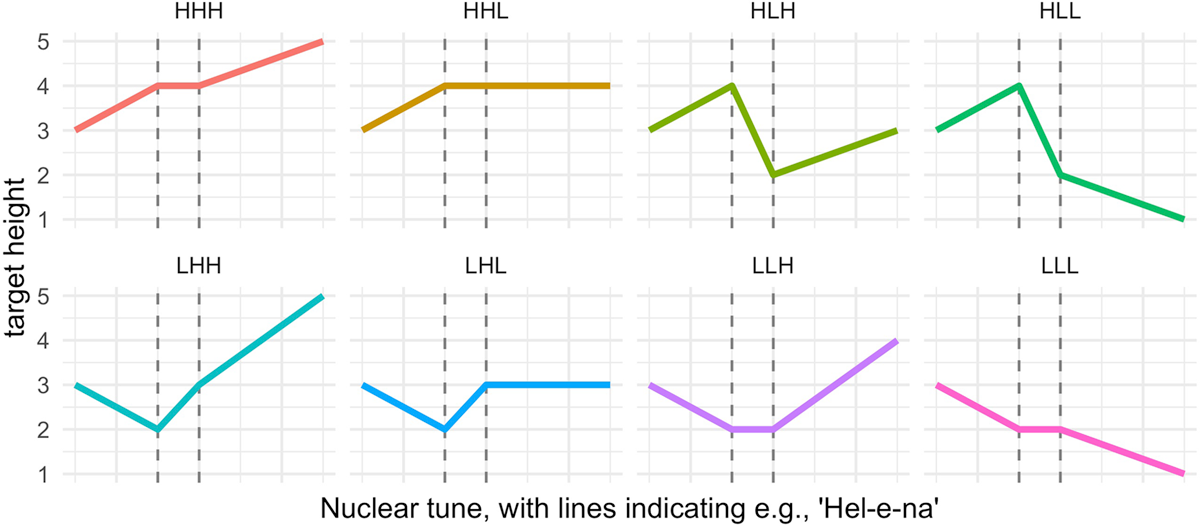
The speech materials used to create the stimuli were spoken by one male and one female speaker of American English. Materials were recorded in a sound-attenuated booth, using a Shure SM81 Condenser Handheld Microphone and Pop Filter, with a sampling rate of 44.1 kHz. From these recordings, we synthesized f0 trajectories for the eight nuclear tunes using a custom Praat script (Boersma & Weenink, 2019). Three sentences, produced by each speaker, were used as source files for the resynthesis. These were: She quoted Helena, He answered Jeremy, and She remained with Madelyn. Each word bearing the nuclear tune (the “nuclear word”), is a trisyllabic stress-initial name in sentence-final position. We refer to the portion of the sentence that precedes the nuclear word as the preamble.
The f0 trajectory of each resynthesized nuclear tune was based on tonal targets and straight-line interpolations between them from the MIT Open Courseware ToBI training materials (Veilleux, Shattuck-Hufnagel & Brugos, 2006), which in turn are based on straight line approximations of naturally produced f0 trajectories in Pierrehumbert (1980, Appendix). Each tune was created based on two parameters: f0 turning points and f0 targets. Turning points are locations where f0 changes direction, which in the resynthesis were anchored to acoustic landmarks in the segmental string. Target f0 heights were established as points within a speaker’s range that sounded natural and were distributed similarly for the male and female speaker (see Table 1, and Figure 1, details in the online supplement).
Target heights (in Hz) for the model speakers.
| Target height | male | female |
| 1 | 80 | 100 |
| 2 | 105 | 160 |
| 3 | 130 | 200 |
| 4 | 225 | 300 |
| 5 | 265 | 380 |
Notice that the model trajectories do not maintain a fixed target f0 height for each pitch accent {H*, L*}, phrase accent {H-, L-}, and boundary tone. Rather, the H/L contrast at each location in the nuclear tune is phonetically implemented with a relative distinction in target f0 height, through the application of context sensitive implementation rules (Pierrehumbert, 1980). For example, a rule of upstep boosts the target f0 height for {H%, L%} following a H- phrase accent, which accounts for the higher-then-expected final f0 in the HHL tune. But following the L* pitch accent in the tunes {LHH, LHL}, the same upstep rule has less of an effect: The tune pair {LHH, LHL} is more distinct in final f0 values than the corresponding pair {HHH, HHL}. These differences in the target f0 for {H%, L%} result from context sensitive implementation of the H/L tonal contrast. The resynthesized trajectories, modeled after those in Pierrehumbert (1980), reflect these implementation rules. We note here that there is not always unanimous agreement about whether these implementation rules fully capture the appropriate acoustic implementation of a given target contour, but the decisions about alignment and scaling of the stimulus utterances used in this study represented a balancing of the requirements for distinctness and appropriateness, in the authors’ judgment.
2.2. Speech production experiment
2.2.1. Participants
We recruited participants from undergraduate students in the Linguistics subject pool at Northwestern University (n = 22), as well as through the crowd-worker platform Prolific (n = 8). We restricted our analysis to participants who were self-reported native speakers of American English with no speech or hearing deficits. Exploratory analyses revealed no discernable differences between these populations, so we pooled them in the analysis. We thus analyzed data from 30 participants.
2.2.2. Procedure
Participants completed the experiment remotely – taking the experiment over the internet on their own computer. They were instructed to be seated in a quiet room and to wear a pair of headphones during the experiment. Participants were told that they would be listening to “computer generated speech” and that they should listen to the model utterances in a given trial and then produce a new sentence with the same melody, but “said the way you think it should sound if it were spoken by a human English speaker”. This instruction was given to encourage participants to modify or enhance their production relative to the model tune, allowing for them to introduce acoustic correlates which were not implemented in the resynthesis. A trial consisted of the auditory and orthographic presentation of the three model sentences, each with the same nuclear tune, and each separated by one second. The target sentence was then presented orthographically, with a reminder presented above it which read “I would say it this way”. The experiment consisted of 144 trials which paired each tune with each of six possible orders of model speaker gender (FFM, FMF, MFF, MMF, MFM, FMM), and all three target sentences. All trials were randomized. The experiment took approximately 30 minutes on average to complete.
2.2.3. f0 measurement and data processing
All audio files were segmented into words using the Montreal Forced Aligner (McAuliffe, Socolof, Mihuc, Wagner & Sonderegger, 2017), which aligned Praat text grid boundaries to word edges. Force-aligned text grids were then audited manually in Praat to ensure that word boundaries were correctly placed. Manual corrections were made when required to ensure that word boundaries were aligned with reliable acoustic landmarks. During this auditing process, files that contained disfluencies, recording errors, audio issues, or incorrect productions of the sentence prompt were excluded (1.8% of the data in total). Audio files and corrected force-aligned text grids were subsequently processed in VoiceSauce (Shue, Keating, Vicenik & Yu, 2011), using the STRAIGHT algorithm to estimate f0 (Kawahara, Cheveigné, Banno, Takahashi & Irino, 2005). We additionally excluded one participant (from an original 31 participants) for whom we could not measure f0 reliably (70% of their sound files contained f0 measurement errors, described below). We excluded inaccurate f0 measures (expected to be present due to non-modal phonation phrase-finally, e.g., Penney, Cox & Szakay, 2020) using an automated method that detected inaccuracies in measurement based on sudden sample-to-sample changes (Steffman & Cole, 2022). 10.7% of the data were excluded due to inaccurate f0 measurement.
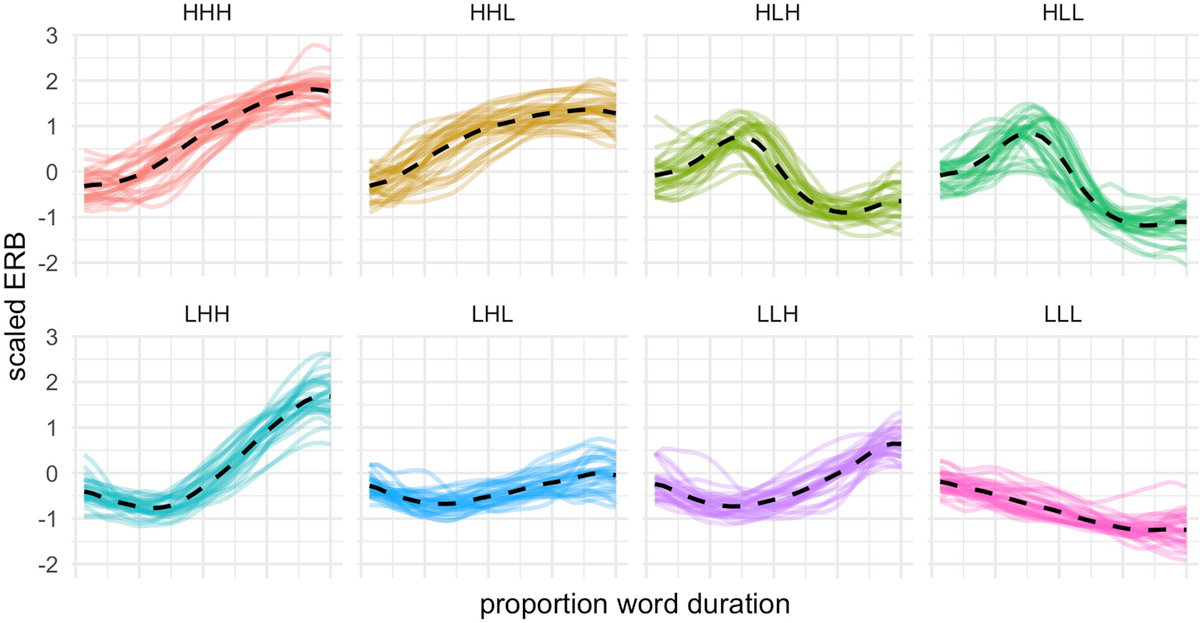
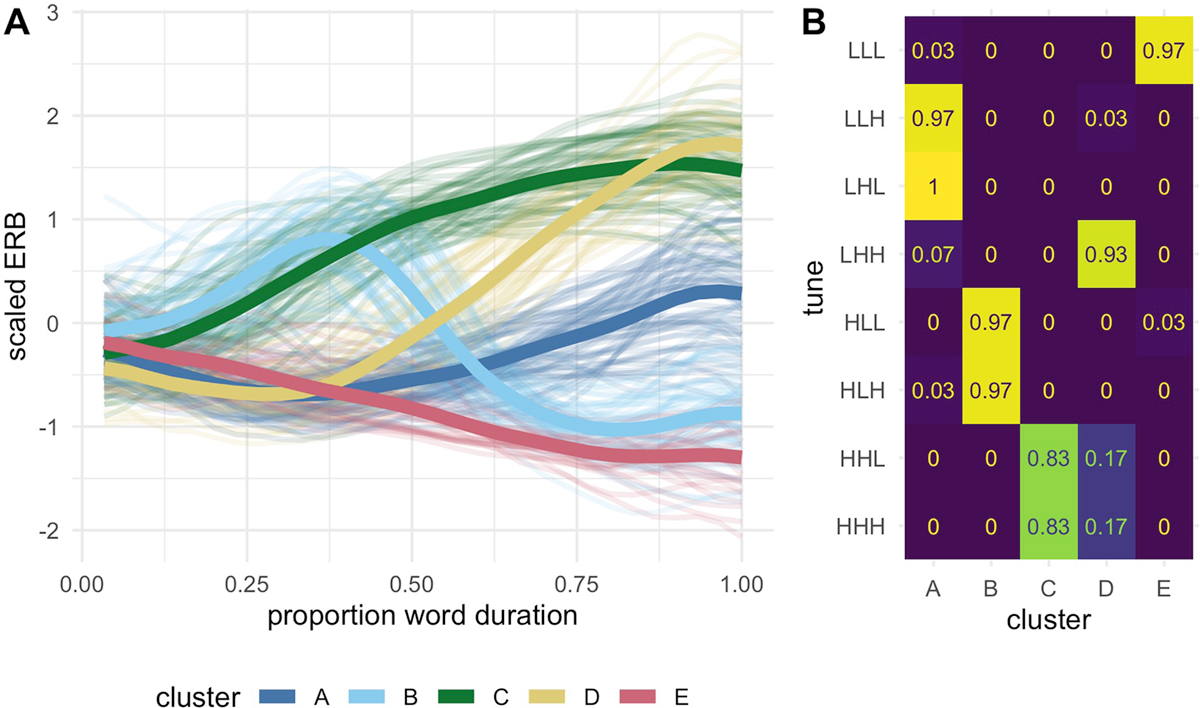
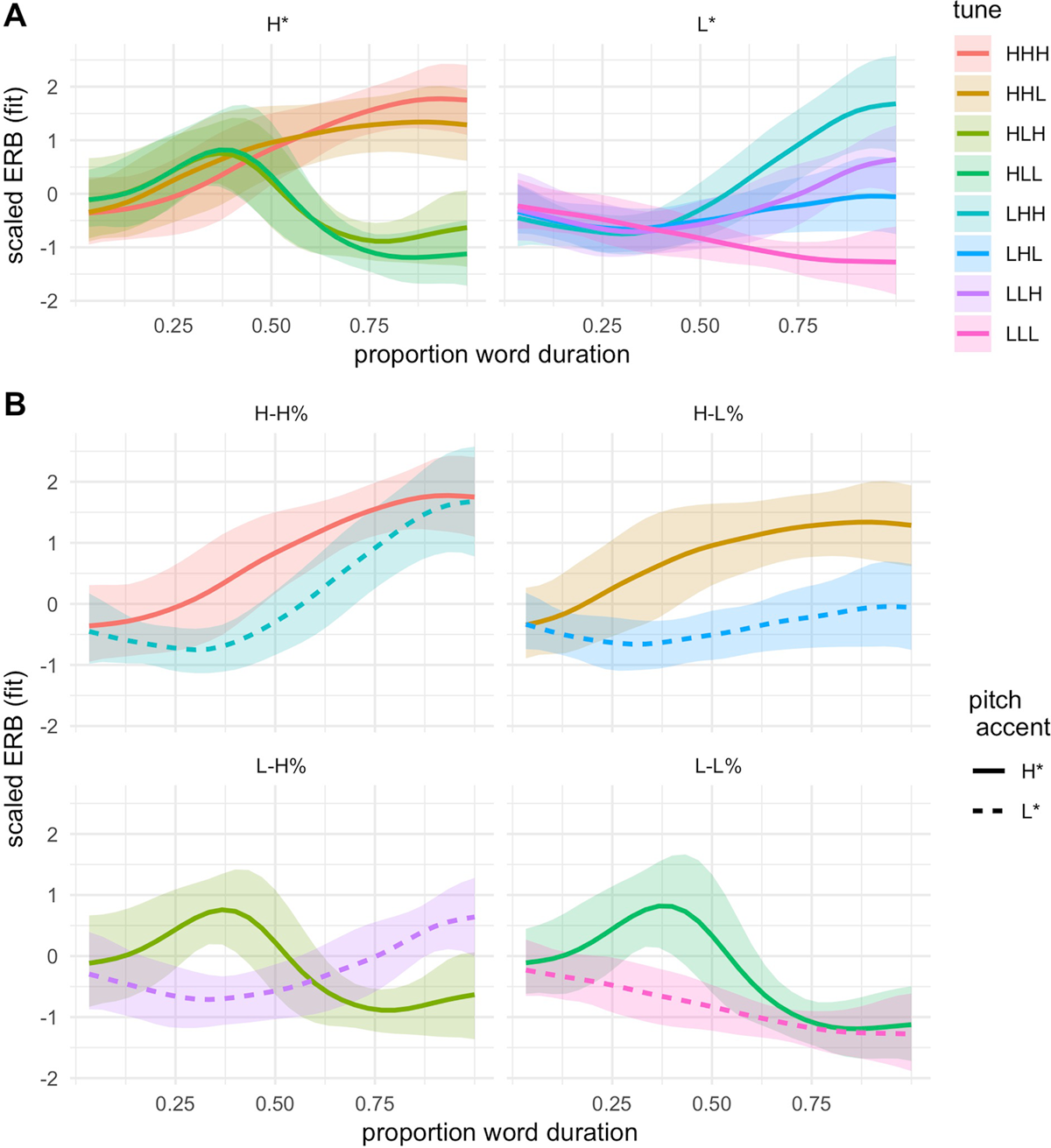
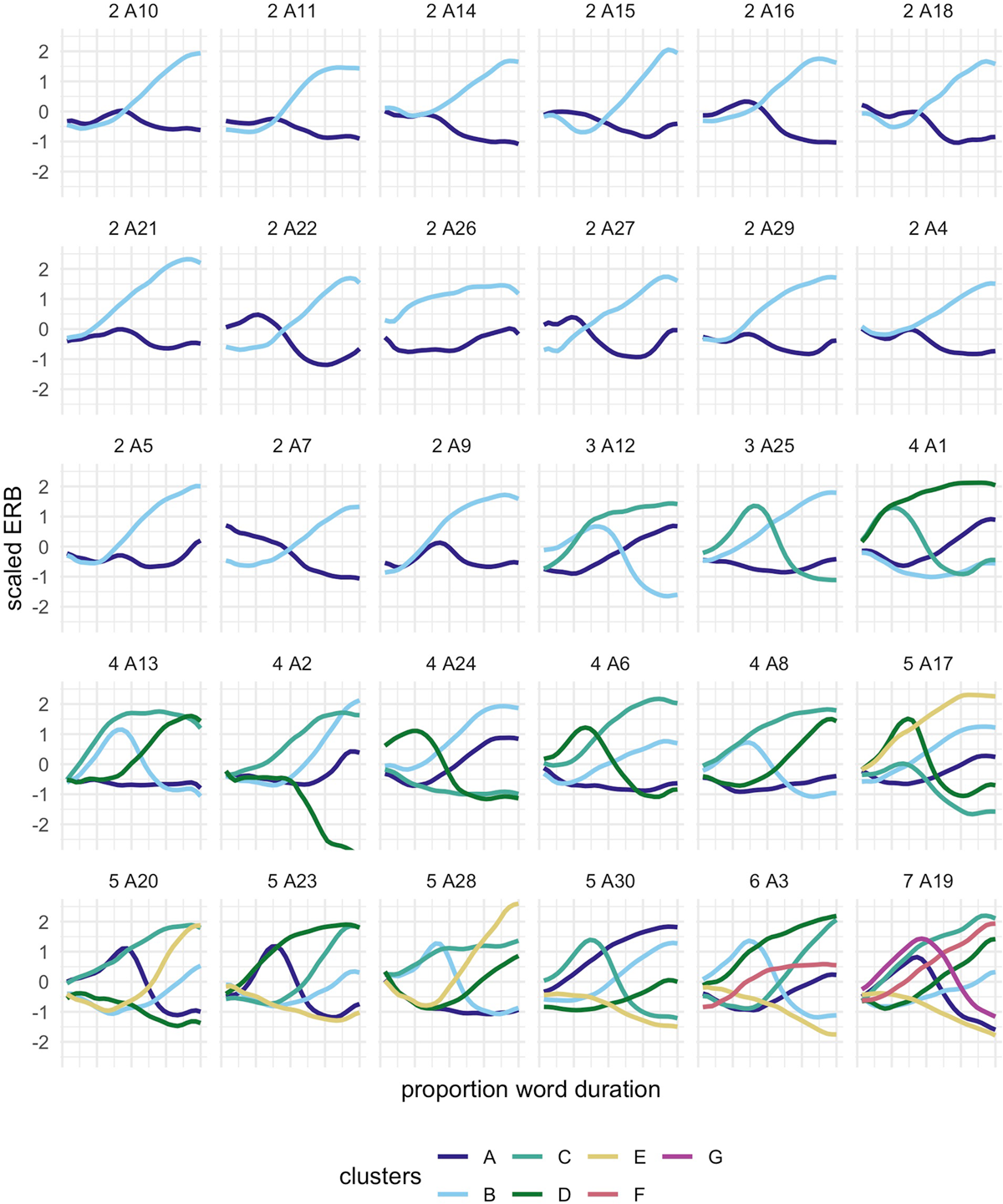
F0 trajectories from the nuclear word were downsampled at 30 equidistant time points, thereby normalizing differences across trials in the raw duration of the nuclear word. Figure 2 shows the mean scaled ERB over normalized time for the eight tunes, excluding trials with inaccurate f0 measures. Note that the imitations reproduce the shape distinctions that generally follow those of the model tunes, though there is clear inter-speaker variation. It also appears that the imitations of some tunes are only minimally different from one another (e.g., HLH and HLL), which we return to below.
2.2.4. Analyses
2.2.4.1. RMSD as a measure of imitation accuracy and tune pair distance
To assess how closely a participant’s reproductions matched that of the model speaker, we computed the root mean squared distance (RMSD) between the f0 trajectories of the participant’s production and the most recently heard model sentence. RMSD was computed in centered (but not scaled) ERB, thus allowing for us to see if the participants accurately reproduced the pitch range of each model speaker, with the female speaker showing an expanded pitch range (see Table 1). RMSD was computed using the standard formula, shown in (1). RMSD provides a measure of the overall acoustic similarity of the imitated tune to the corresponding model tune, in terms of the difference in f0 space between the two at each sample. RMSD has also been shown to be a significant predictor of perceptual judgments of similarity for f0 trajectories (Hermes, 1998; based on ratings from experienced phoneticians), a finding that is also confirmed in our results (with similarity rated by untrained listeners).
- (1)
In (1), xi is the centered ERB of a speaker’s production at time n (for 30 time-normalized samples per nuclear word), and yi is the model speaker’s centered ERB at the corresponding normalized time. For each trial we thus obtain a single RMSD value, which is a larger value when the speaker deviates more from the preceding model. For the purpose of statistical modeling, these by-trial RMSD values (not the f0 trajectories themselves) were subsequently centered on the grand mean RMSD (over all trials and speakers). We will refer to this as accuracy in the sense that it reflects the participants’ accuracy with respect to the model tune on a given trial.
We also used the RMSD formula in (1) for several additional metrics. First, for a given participant, we computed the mean trajectory of each tune, and then using the RMSD equation in (1) we calculated the acoustic distance between all pairwise combinations of tunes for a given speaker (e.g., HHH vs. HHL, HHH vs. HLH, and so on). This will be referred to as distance, as it reflects the distance in acoustic space between pairs of tunes. A larger distance corresponds to a bigger acoustic distinction between a given pair of tunes. Finally, we applied the same approach to capture the differences between pairs of model tunes. Recall that each model tune was instantiated over six unique stimuli (three words, two speakers). We scaled these measures by speaker, and then computed the mean for each tune. The result was eight trajectories based on scaled ERB. From these pairs we then computed RMSD for all possible pairwise combinations. These scaled-ERB-based values principally capture shape distinctions among the eight tunes, which we expect to be important for perception discrimination, thus relevant for describing differences in the model tunes. Here again a larger RMSD value corresponds to a bigger difference between model tunes. We compare the distances between pairs of tunes for participants and models to one another in Section 3.1.1. to assess if participants are generally matching the models in terms of the separation of tunes in f0 space. Notably, in Figure 4 below, and only there, we present unscaled model distance RMSD values, which we compare to unscaled speaker distance RMSD values.6
Variation in (centered) accuracy RMSD was modeled using a linear mixed-effects model implemented in brms (Bürkner, 2018), with predictors of tune, participant gender, and model speaker gender. We fit the model with weakly informative priors using normal distributions, specified as Normal(0,1), for the intercept and fixed effects. Tune and model speaker gender were both contrast (sum) coded. The random effects structure of the model included an intercept for speaker, and a by-speaker slope for tune and model speaker gender.
For all mixed-effects models reported here, all run in brms, we fit the model to draw 5,000 samples in each of four Markov chains, with a burn-in period of 1,000 iterations in each chain (80% of samples retained for inference). R̂, Bulk ESS, and Tail ESS values were examined to confirm convergence and adequate sampling. In reporting results from Bayesian models, we give the posterior median estimate and 95% credible intervals (CrI). When these intervals exclude the value of zero, they provide compelling evidence for an effect, i.e. a clearly non-zero effect size (e.g., Vasishth, Nicenboim, Beckman, Li, & Kong, 2018). For the purposes of effect interpretation, we focus on effects which meet this criterion. Where relevant, we additionally provide the pd metric as computed with the bayestestR package (Makowski, Ben-Shachar, & Lüdecke, 2019). This represents the percentage of the posterior, which shows a given directionality ranging between 50% (a distribution centered exactly at zero: No effect) and 100% (a distribution which excludes zero entirely: A clear effect). pd values larger than 95% can be taken as evidence for an effect. Full models and model summaries are included in the open access repository, and we report just the effects of interest in the text of this paper.
2.2.4.2. Clustering analyses
For an answer to the question of whether there is an eight-way distinction among the f0 trajectories produced as imitations of eight model tunes, we use clustering analyses to evaluate the similarity-based grouping of the imitated f0 trajectories. This analysis does not impose any restrictions on how f0 trajectories may be distinguished from one another, nor does it consider the phonological label of the model tune (e.g., in terms of H and L tone features) that was the intended target of imitation for any given f0 trajectory. Rather, it identifies the distinctions among imitated f0 trajectories that are sufficiently robust to define distinct clusters over the entire dataset. We inspect the output of the optimal clustering solution to determine how the emergent clusters relate to the eight model tunes, asking if imitations of a given tune are assigned to the same cluster, and qualitatively evaluating the shape of the average trajectory for each emergent cluster. Clustering analyses were performed over the time-normalized f0 trajectories using k-means clustering for longitudinal data (KML cluster analysis) with the R package kml (Genolini, Alacoque, Sentenac & Arnaud, 2015).7
The clustering algorithm operates by comparing, for the same dataset, clustering solutions using different numbers of clusters. Each clustering solution represents the optimal grouping of observations (i.e., f0 trajectories, each represented as a vector of 30 f0 values) into k clusters, minimizing within-cluster variance while maximizing between-cluster variance based on Euclidean distances. The optimal number of clusters was determined using the Calinski-Harabasz criterion (Caliński & Harabasz, 1974), to identify the value of k (between two and eight clusters, for our data) that yields the highest ratio of between- to within-cluster variance.8 One clustering analysis was performed on the mean f0 trajectories calculated for each speaker and exposure tune in scaled ERB, such that each participant contributed eight trajectories to the analysis (one trajectory for each of the eight tunes). Additional clustering analyses were performed separately for each speaker, over each imitated trajectory (i.e., each trial).
2.2.4.3. Machine classification
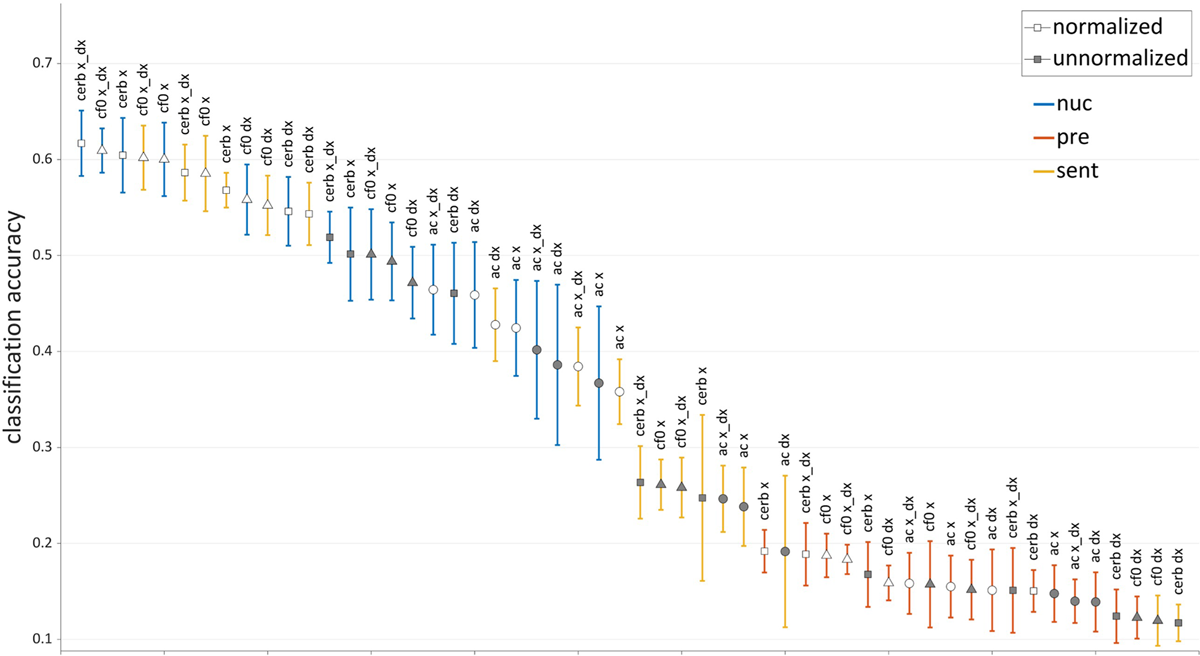
The clustering analysis allows us to examine the similarity-based grouping of imitated f0 trajectories without regard for how the emergent clusters relate to the distinct f0 trajectories present in the model tunes. But we are also interested to know how well the imitations preserve the specific eight-way distinction among the model tunes. In other words, we want to know if the imitated f0 trajectories of a given tune (e.g., HLL) are similar to one another and distinct from the imitations of other tunes. We address this question using a bidirectional LSTM (long short-term memory) neural net classifier trained to assign imitated f0 trajectories to one of eight classes corresponding to the exposure (model) tune labels. LSTMs are a type of recurrent neural network that perform especially well to classify sequence data, as they can learn dependencies between values at different time steps, which are not captured in the cluster analysis. The classifier is trained and tested on the imitated f0 trajectories, trained on labeled data (imitations identified by the label of the exposure tune), and tested on unlabeled data. Average classification accuracies for each tune category, along with average between-category misclassification rates, were calculated over 20 repetitions of a training-testing procedure. In each repetition, the data were randomly partitioned into training (45%), validation (10%), and test (45%) subsets. The eight tune categories were balanced within each subset. The classification networks consisted of an input layer and two bidirectional LSTM layers of 200 units, each followed by a 50% dropout layer. These were followed by a fully connected layer, a softmax layer, and a classification layer. The Adam training algorithm was used (Kingma & Ba, 2014) with L2 regularization 0.001, learning rate 0.0001, and validation patience 20 epochs. Various input representations of the f0 trajectory were tested.9 Here we report only the combination of parameters that yielded the highest average accuracy in classification: Time-normalized ERB at two successive time steps (x & dx), in the nuclear word only.
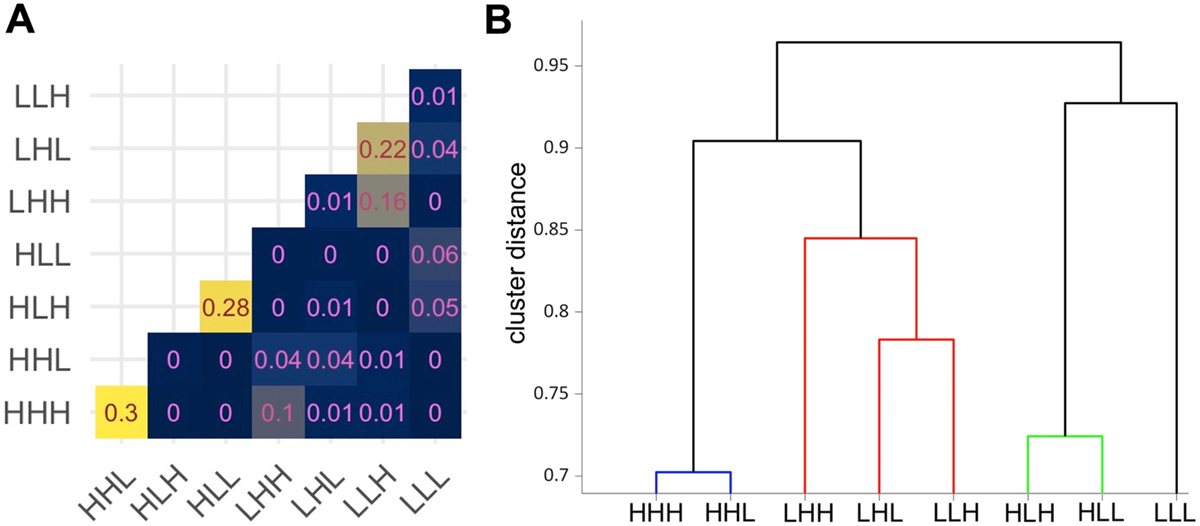
Inspecting the misclassified imitations reveals which tunes were confused with which other tunes. We used agglomerative hierarchical clustering to infer groupings among the imitations of the eight tune classes based on the average proportions of misclassified trials, using the distance metric δ(A, B) = 1 – P(A, B), where P(A, B) is the proportion of trials where tune A is classified as B. Tune pairs that are more often confused in the classifier output will be separated by smaller distances in the hierarchical clustering analysis. The overall hierarchical structure shows how the eight tune classes are dispersed in the f0 space of the imitated trajectories.
2.2.4.4. Fine-grained acoustic variation: GAMM modeling, f0 turning point, and duration analysis
Looking beyond the similarity-based grouping and classification of imitations, we are interested in examining whether the imitations preserve, to any degree, predicted distinctions among f0 trajectories, reflecting the distinctive properties of the model tunes. We are especially interested in examining imitated f0 trajectories for tunes that appear to merge with other tunes in the clustering and classification analyses (i.e., tunes whose imitations are grouped in the same cluster, and which are confused for one another in the classification analysis), to see if predicted differences can be detected, however small they may be. We first modeled the entire f0 trajectory of each tune, based on its imitated productions, using a generalized additive mixed model (GAMM). In the analysis of f0 trajectories, GAMMs can be used to test for significant differences between trajectories belonging to two (or more) groups, which in our case are the eight tunes. The model was fit to predict scaled ERB over normalized time (in 30 samples), using the R packages mgcv and itsadug (van Rij, Wieling, Baayen & van Rijn H, 2020; Wood, 2017). The GAMM was fit with parametric terms for tune category (coded with HHH as the reference level), and smooth terms for tune category over time. Random effects were specified as reference/difference smooths for speaker and tune, following Sóskuthy (2021). The default number of basis functions for each smooth term were found to be adequate, as determined by the gam.check() function. From the model fit to all eight tunes, we examine smooth fits and differences for comparisons of interest, as guided by the results of the foregoing cluster analysis. As the coefficients for the parametric or smooth terms are not particularly informative for the questions we ask here (Sóskuthy, 2021), we rely on visual inspection of GAMM predictions to evaluate significance. The full model can be found on the open access repository.
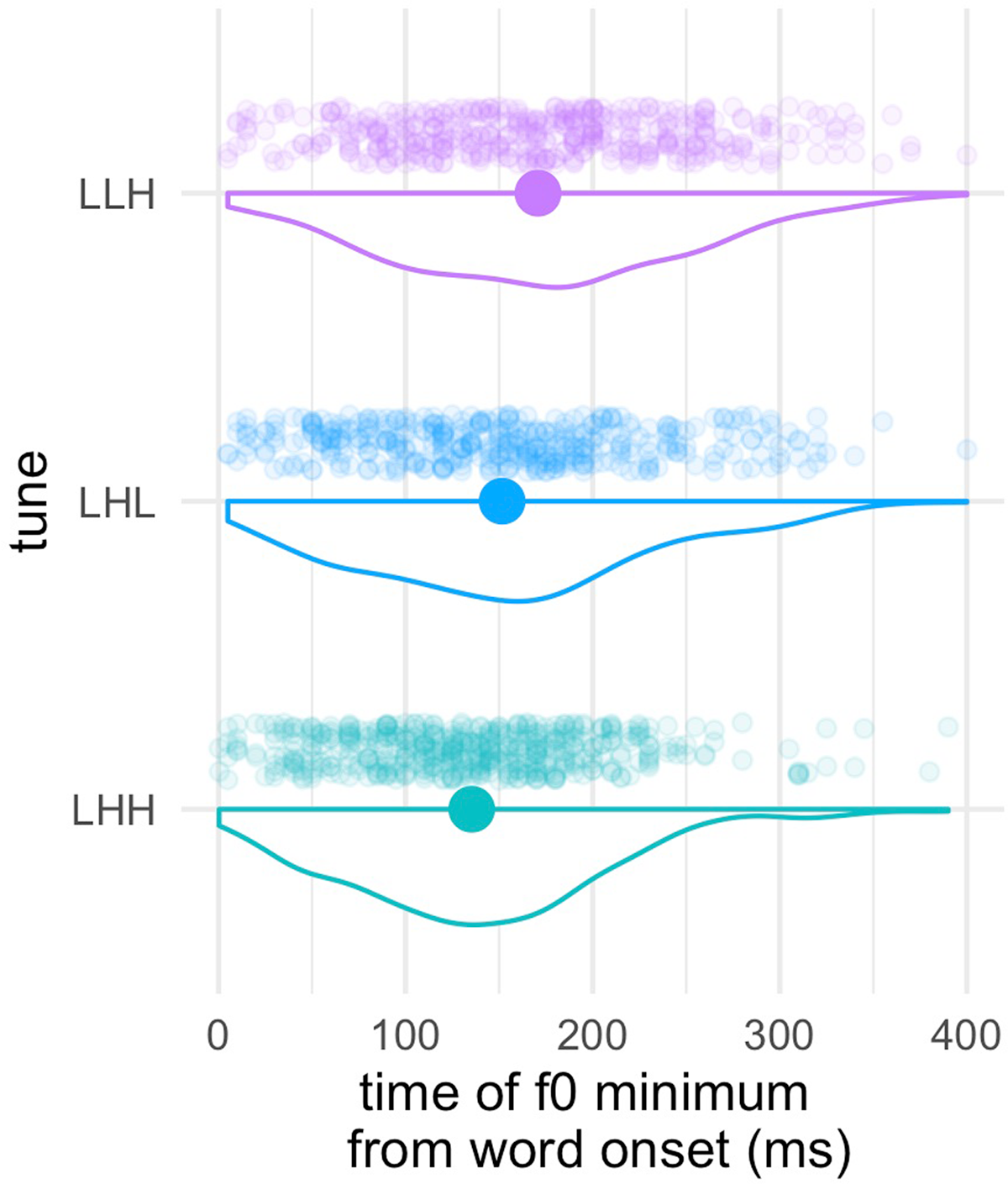
The second acoustic measure we examined was the temporal alignment of the f0 minimum corresponding to the onset of the accentual rise (i.e., the “elbow”), for three tunes that are predicted to exhibit a rise following a Low target: LHH, LHL, and LLH (see Figure 1). We measured the temporal location of this turning point with respect to the onset of the nuclear word. Variation in turning point alignment was modeled using a linear mixed effects regression, as implemented in brms (Bürkner, 2018). The model was fit to predict the time in milliseconds from the beginning of the word to the minimum f0 in the trajectory. The dependent variable was not centered, in order to keep a representation of the raw time to the start of the word. The fixed effect of tune was coded with LHL as the reference level. The random effect structure of the model included an intercept for speaker, and a by-speaker slope for tune. We fit the model with weakly informative priors using Normal(150,100) for the intercept (that is 150 ms from word onset as the center of the distribution), and (0,100) for the fixed effects of tune. The intercept value for the prior was determined based on the mean value for the dependent variable for the reference level tune LHL, which was approximately 150 ms. We opted to model the dependent variable as non-centered to get a more direct assessment from the model estimates in terms of the actual timing for each of the three tunes.
Finally, we examined the duration of nuclear words as a function of tune. We measured word duration for the nuclear word from the force-aligned and manually checked text grids and submitted these measures to a Bayesian linear mixed effects model that predicted word duration (centered) as a function of tune (contrast coded) nuclear word (contrast coded) and the interaction of these two fixed effects. Random effects included a by-speaker random intercept and by-speaker random slopes for both fixed effects. We set weakly informative and normally distributed priors for both the intercept Normal(0,100) and fixed effect Normal (0,100) in ms values.
2.3. Perceptual discrimination experiment
2.3.1. Materials
This experiment used the same 48 stimuli as those used in the production experiment (8 tunes * 2 speakers * 3 sentences). For the AX perception task, we paired together stimuli that varied only in tune. Thus, in a given trial, participants would hear two utterances produced by the same speaker, with the same sentence, but with a (potential) difference in the tune. We combined all tunes with each other in all possible orders, creating 64 (8*8) tune pairs, which included tunes paired with themselves in “same” trials. These pairings were repeated twice, for a total of 128 trials in the experiment. Given these 128 pairings, we created three counterbalanced lists, which combined tunes in various ways with both model sentences and model speakers (see online supplement for details). The result of this process was three lists, each of which contained two repetitions of all possible order-sensitive tune pairings, which were counterbalanced for model sentence and randomly assigned a speaker gender with the constraint that gender was split evenly across all trials.
2.3.2. Participants
We recruited 30 participants for the perception experiment, using the crowd-worker platform Prolific. All participants were self-reported monolingual native English speakers with no hearing or vision problems, and none had participated in the speech production experiment in our study.
2.3.3. Procedure
Participants completed the experiment remotely and were asked to do so in a quiet location while wearing headphones. Each participant was assigned one of the three lists (10 participants per list). Participants were instructed that their task was to listen to the stimuli, and, focusing on the melody, to decide if the utterances they heard were the same or different. Participants indicated their response by clicking on a button, which was labeled “same” or “different”. These buttons were displayed on either side of the monitor, with button placement roughly counterbalanced across participants (the buttons remained on the same side over the course of the experiment for a given participant). During a trial, the text of the sentence would appear at the top of the screen, and simultaneously the two stimuli for the trial would play in succession, separated by an inter-stimulus-interval of 500 ms. Participants then clicked one of the two response buttons and the next trial began automatically. In addition to the 128 test trials, presented in randomized order to participants, there were four catch trials, which gave an auditory prompt to click on either the “same” or “different” button (two of each). These four trials were distributed evenly, though in random order, throughout the experiment. All participants responded correctly to all catch trials.
2.3.4. Analysis
The analysis of participant responses in the perception experiment was carried out by modeling the log-odds of a ‘different’ response using a mixed-effects Bayesian logistic regression, implemented in brms (Bürkner, 2018). We predict this dependent variable by tune pair to assess if certain pairs are discriminated at or below chance, with a random intercept for participant. We specified the model with weakly informative priors, as Normal(0,1.5), in log-odds space, for both the intercept and the fixed effects.
3. Results
3.1. Speech production experiment
3.1.1. Imitation accuracy and distance
In this section we consider how accurately participants reproduce the f0 trajectories of the model tunes, using the accuracy metric. We also consider how participants distinguished pairs of tunes as compared to the model stimuli for the same tune pair, using the distance metric.
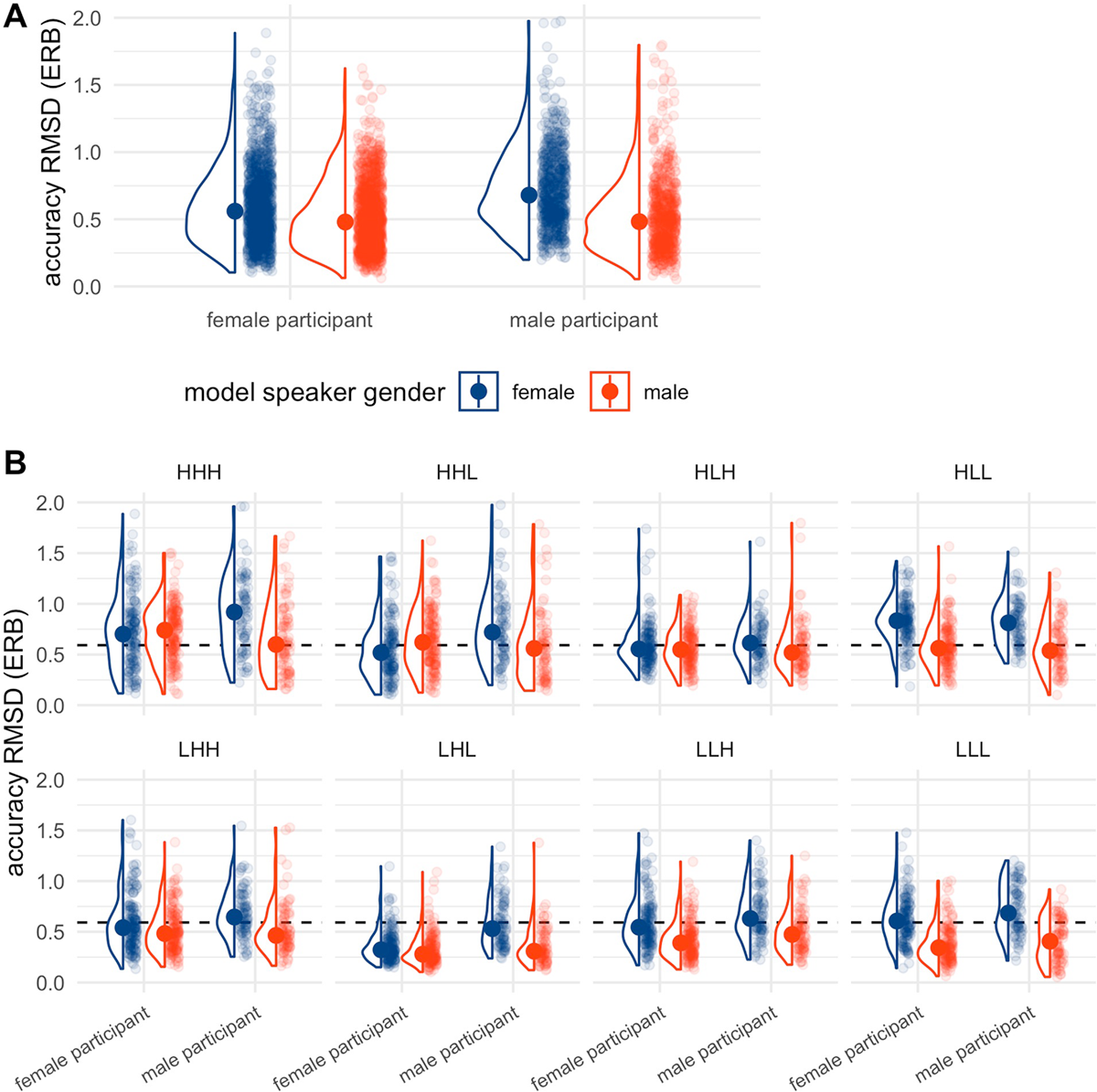
First, considering the accuracy results, we examine whether participants reproduce the precise f0 target values of the male and female model speakers, preserving the f0 range difference between the two. We report results from the model of imitation accuracy in terms of RMSD between the model and imitation on each trial, as a function of model speaker gender (male or female), the participant’s self-reported gender (male or female), and tune. As shown in Figure 3a, there was a main effect of model speaker gender (β = –0.14, 95CrI = [–0.17, –0.11], pd = 100), whereby imitations were more accurate with respect to the male model speaker (having lower RMSD). There was additionally a main effect of participant gender whereby male participants were less accurate overall (β = 0.08, 95CrI = [0.01, 0.16], pd = 99). There was also an interaction of model speaker gender and participant’s self-reported gender (β = –0.10, 95CrI = [–0.16, –0.04], pd = 99). Using emmeans (Lenth, 2021), we examined the interaction by extracting marginal estimates for the effect of participant gender within model gender.10 This examination showed that for the male model speaker there was not a credible difference in accuracy as a function of participant gender: Male and female participants were not reliably different from one another (β = –0.03, 95CrI = [–0.10, 0.04], pd = 79). In comparison, for the female model speaker there was a difference in accuracy as a function of participant gender (β = –0.13, 95CrI = [–0.21, –0.05], pd = 100), whereby male participants were less accurate than female participants. Examining the interaction thus suggests that the main effect of participant gender is driven by imitations of the female model speaker. Figure 3B shows the same effect but split by tune. Here we simply note that accuracy varies by tune overall, as does the effect of model speaker gender and the interaction with participant gender.
Accuracy (RMSD) with respect to the most recently heard model speaker, as a function of participant gender and model speaker gender (Panel A) and split by tune (Panel B). Violin plots show the distribution, and light points show each observation. The larger solid point indicates the mean. In Panel B, the dashed horizontal line indicates the grand mean RMSD as a point of reference.
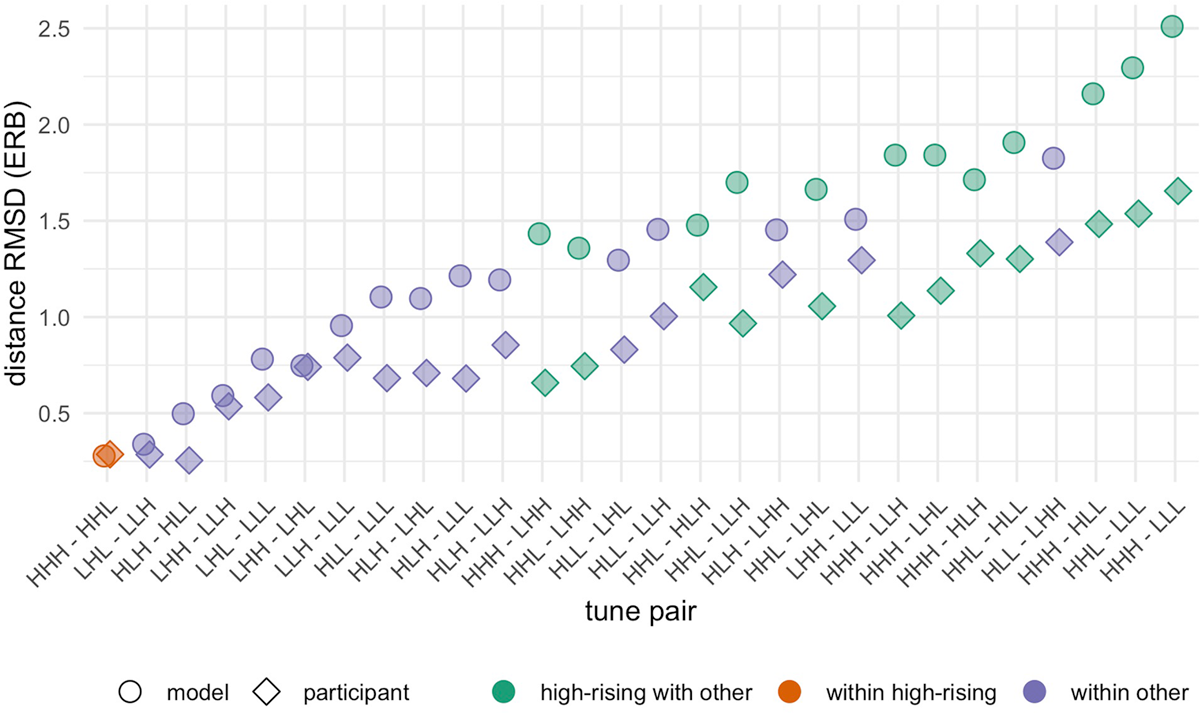
Distance (RMSD) between tune pairs as produced by participants (diamond shape), and as present in the model stimuli (circle shape). All values are computed from centered (and not scaled) ERB. Tune pairs are sorted from low to high and colored by whether a member of the pair is {HHH, HHL}, described in the text.
Next, we briefly consider the distance results, shown in Figure 4. These values are critically left unscaled here to capture actual variation in height and vertical displacement of centered trajectories, both for models and speakers. We first note that distance varies by tune pair (left to right along the plot), and the participants generally produced tunes as less separated in f0 space (less distance between pairs of tunes) relative to that of the models. The coloration of the points on the plots also indicates whether a tune pair includes one of the High-Rising tunes {HHL, HHH}, which will be shown to be robustly distinguished from other tunes in the results that follow. Anticipating these results, we note that tune pairs in which just one member is HHH or HHL (“high rising with other”) tend to have both higher participant distance (greater distance between tunes in participant imitations), and model distance (greater distance between that pair in the stimuli). The “within other” class tends to have smaller distances for both participant and model tunes. That is, tune pairs that do not include one of {HHH, HHL} tend to show smaller distances than tune pairs that do include one of these High-Rising tunes. Finally, we note that participants do not deviate in a uniform way from the model stimuli; the difference between distance values for a given tune pair is not always higher for the model stimuli, though it usually is.
In total, the accuracy results show clear effects of model speaker gender, and participant gender, both indicating that listeners are not imitating all aspects of the model stimulus. If participants were imitating the phonetic detail for each stimulus, there should be no main effect of model speaker on accuracy. Instead, we see that both male and female participants are less accurate with respect to the female model speaker (shown in Figure 3A), who has an expanded pitch range. We further see that participants’ self-reported gender interacts with the effect in an expected way: Male participants are even less accurate with respect to the female model speaker. The distance results complement this conclusion in showing that the acoustic distance between tunes is generally reduced for participant productions as compared to the models. Variation in the differences between participant and model distance values further suggests that certain tune pairs are reproduced in a way that differs from the models. These results are taken as evidence that participants are not merely parroting the f0 trajectories they hear.
3.1.2. Group-level clustering
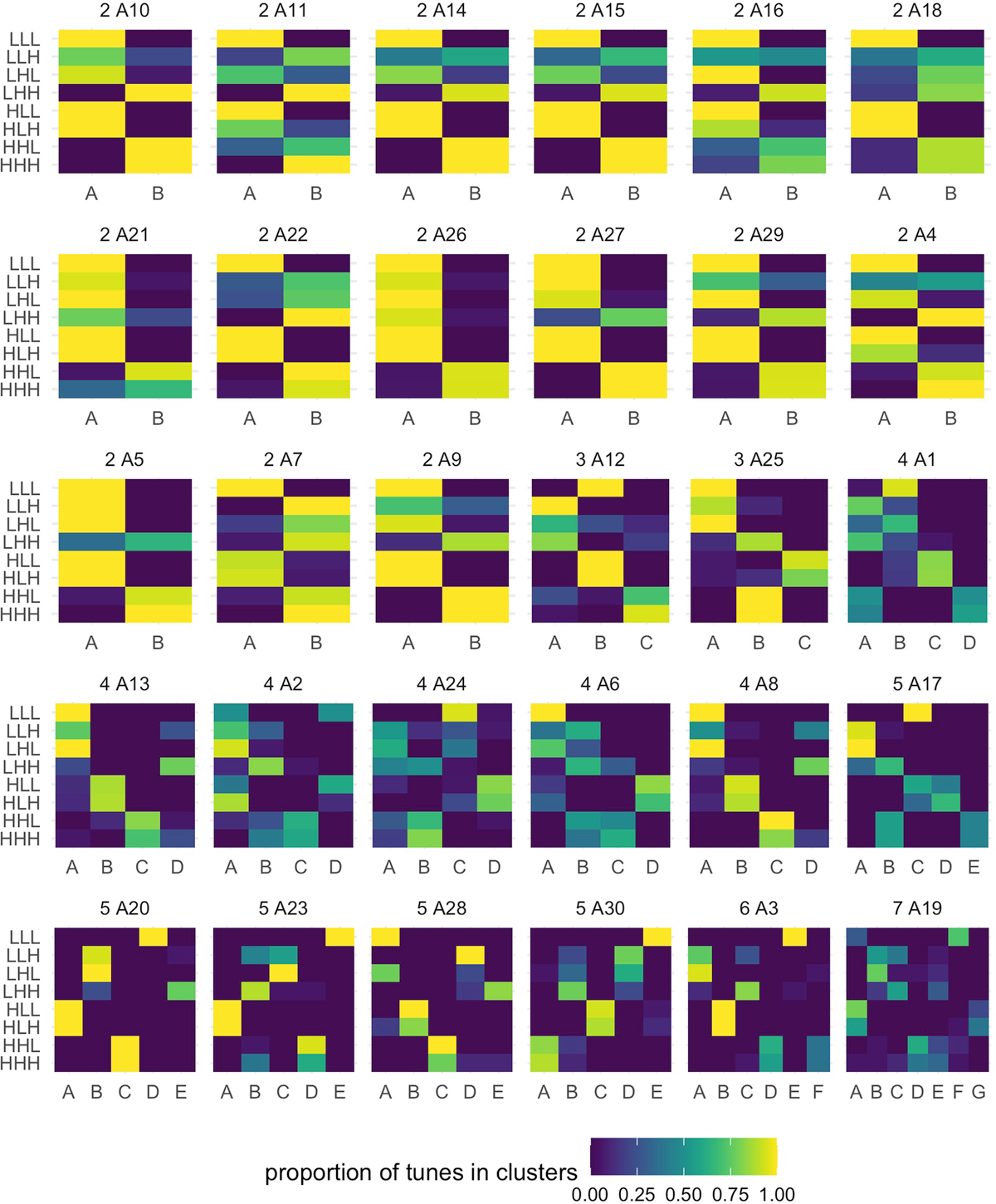
We next consider how the unlabeled f0 trajectories (participant means by tune, eight trajectories per participant) cluster together and the mapping between tune labels and clusters. The results from this analysis address the question of how imitations of a given tune map onto clusters defined by the k-means clustering analysis. The result from the clustering analysis identifies five as the optimal number of clusters for the data (labeled A-E in Figure 5). Figure 5A plots the five emergent clusters in normalized time, with the mean f0 trajectory for each cluster shown as the dark-colored line. Figure 4B is a heat map showing the composition of each emergent cluster in terms of the proportion of imitations of each tune that are grouped into that cluster. With respect to the mean trajectories, Cluster A can be described as a shallow low-rising cluster, and as shown in the heat map, it is made up of imitations of two tunes: LHL and LLH, two low-rising tunes that were entirely (LHL) or nearly entirely (LLH) placed in this cluster. Cluster B can be described as the rising-falling cluster and exhibits a similar collapse of two model tunes, with almost all imitations of HLL and HLH placed in that cluster. In a similar fashion, HHL and HHH are largely collapsed into Cluster C, a high-rising cluster; however, both tunes also contribute to a smaller degree to Cluster D, with a scooped rising shape, which is otherwise made up of mostly LHH. Note that Cluster D is similar in shape to Cluster A, but with a steeper rise and higher final f0 compared to Cluster A. Finally, Cluster E, a low-falling cluster, is made up almost entirely of LLL. Overall, the f0 trajectories produced as imitations of eight input tunes define five clusters, three of which essentially collapse a distinction between two model tunes.11
Cluster means (dark lines) and contributing trajectories (light lines) for each of the five clusters (Panel A), and the proportion of the imitations of each tune that contributed to each cluster (Panel B), where columns indicate clusters, and rows indicate tunes. Coloration on the heat map indicates the proportion of tunes in each cluster, which is also labelled numerically.
3.1.3. Neural net classification
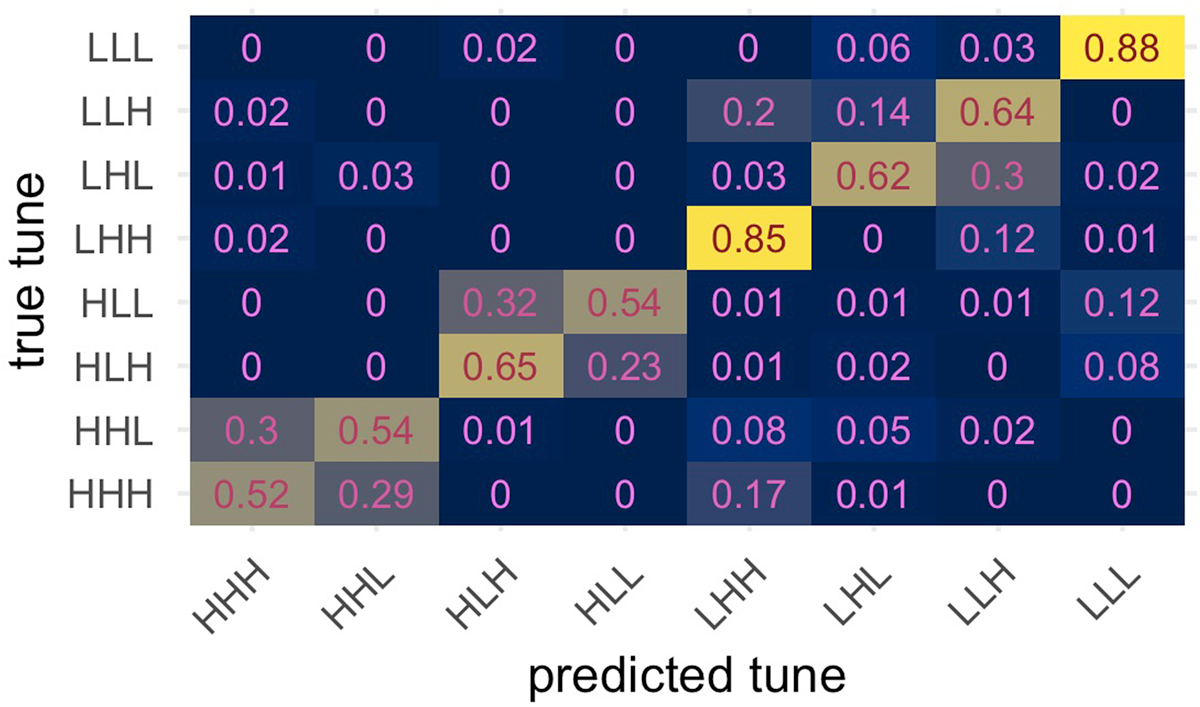
Neural network classification accuracy of the imitations is high overall, with 65% correct classification of f0 trajectories into classes corresponding to the eight model tunes (chance = 12.5%, or 0.125), as shown in the confusion matrix in Figure 6.
However, certain tune pairs were frequently confused, as shown in the confusion matrices over tune pairs in Figure 7A, where each cell shows the average of confusions between two tunes in Figure 6. From Figure 7A, the imitations of four pairs of tunes stand out as being the least well-classified. These pairs are: {HHH, HHL}, {HLH, HLL}, {LHL, LLH}, and {LHH, LLH}. Taking pairwise classification accuracy as a kind of distance measure, tunes can be grouped together in clusters, as shown in the hierarchical clustering diagram (Figure 7B). The tunes in the High-Rising class {HHH, HLL} are the least separable (smallest distance on the vertical axis), followed by the rise-fall pair {HLH, HLL}, and low-to-mid rising pair {LHL, LLH}. The low-to-high rising tune LHH joins the shallow low-rising pair to form a broader similarity grouping of low-rising tunes. The low-falling/flat LLL tune stands alone with the greatest distance from all other tune clusters, with imitations of LLL rarely being misclassified. These results suggest a mapping of imitated tunes onto a similarity space in which the four most distant clusters are described in terms of their holistic shape: High-rising, rise-fall, low-rising (which may further be separated into LHH versus {LHL, LLH}), and low-fall/flat. Within a cluster, tunes with distinct tone labels are separated by a very small distance and are often misclassified for one another.
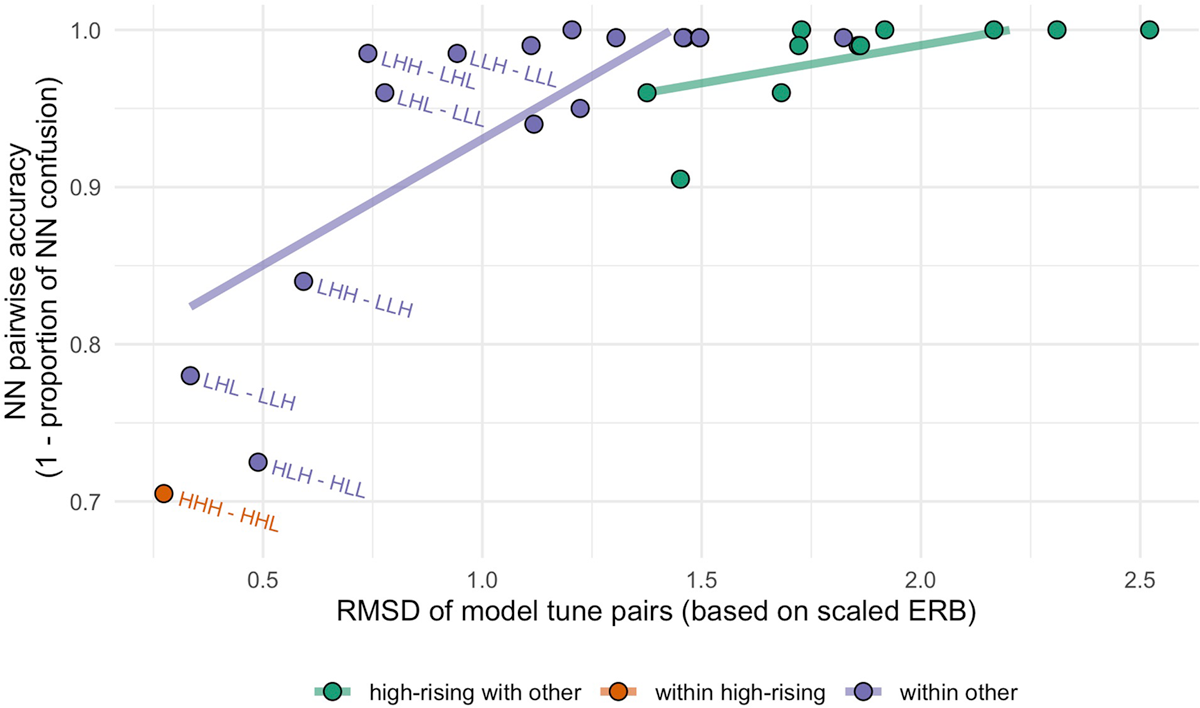
Figure 8 plots NN accuracy for tune pairs (1- the confusion rate plotted in Figure 7) against the distance (RMSD) between pairs of model tunes (same measure from Figure 4). As with Figure 4, points are colored by whether they include a member of the set {HHH, HHL}. Figure 8 shows a general relationship between the distance between the model tunes and the NN classification of the imitations of those tunes; however, it is clear that pairs that compare a member of the High-Rising class with another tune show near-ceiling NN accuracy, with a minimal effect of pairwise distance (shallow slope for the green regression line). On the other hand, pairs that are in the Within-Other category show a stronger relationship between model distance and NN accuracy. This offers some preliminary evidence that particular tune comparisons are more robustly distinguished than others, and less related to the pairwise distance between model tunes, which we return to below.
The NN classification results converge on the same findings obtained from the clustering analysis, both showing evidence for weak pairwise distinctions for four tune pairs. Notably, all four collapsed/confusable tune pairs vary primarily in the f0 value at the end of the tune, as shown in the model tunes (Figure 1). Put differently, what the tunes in each collapsed/confusable pair have in common is their shape at the beginning of the nuclear word, including the f0 movement associated with the pitch accent.
3.1.4. GAMM modeling analysis
Both the clustering analysis and neural net classification analysis show a loss of distinctions in the imitations for some of the eight model tunes tested. But those results don’t rule out the possibility of there being fine-grained differences among imitations that may not be sufficient to support clustering or classification, but which nonetheless align with the predicted differences in f0 trajectories among the model tune categories. This section and the following one report results from acoustic analyses that test for such differences, comparing acoustic measures between imitations of different model tunes. We begin with the GAMM modeling results.
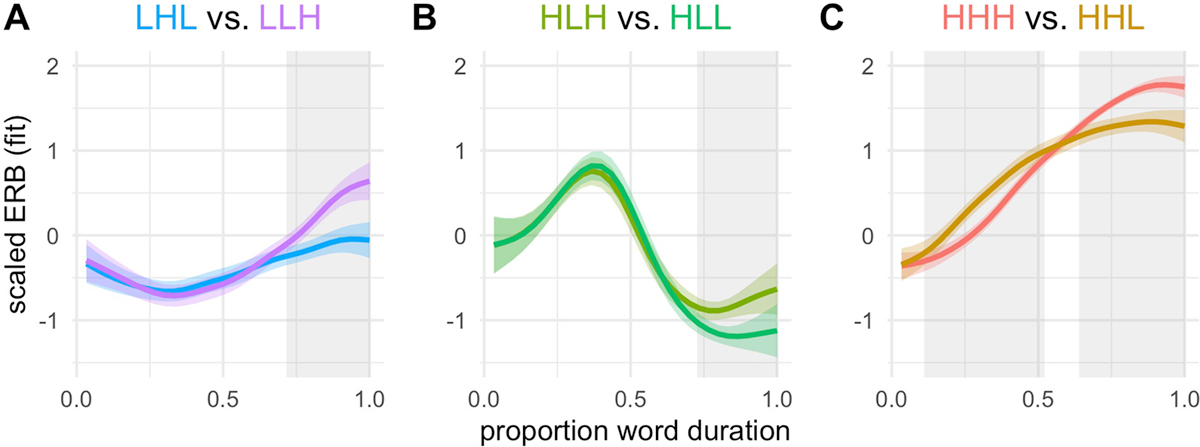
The imitated f0 trajectories were submitted to a GAMM model to test for differences based on the label of the exposure tune from each trial. Figure 9 shows the mean trajectories (with shaded regions marking one standard deviation around the means) from the GAMM model for each of the eight tunes. The predicted trajectories are grouped by pitch accent {H*, L*} in Panel A, and by edge tone sequence {H-L%, H-H%, L-L%, L-H%} in Panel B. These modeled f0 trajectories bear a strong resemblance to the model tune distinctions overall (Figure 1), but unsurprisingly, there is also notable overlap in the modeled trajectories (i.e., overlap in the shaded regions around mean trajectories). These figures thus highlight the high degree of variability in the data, with a notably large overlap between three tune pairs that cluster together: {HHH, HHL}, {HLH, HLL}, {LHL, LLH}.
To assess differences among these three pairs of tunes in the GAMM fit, we visualize the fit smooths and corresponding 95% confidence intervals around the mean trajectories. We also examine pairwise difference smooths for tune pairs of interest. The panels in Figure 10A–C plots GAMM fits (same as Figure 9), though this time with 95% CIs from the model. Gray shading shows the region(s) in normalized time in which there is a detectable difference between trajectories, corresponding to areas in which the 95% CIs for difference smooths excluded the value of zero (as described in e.g., Sóskuthy, 2021); these are regions in which we can be confident the difference between a pair of tunes is non-zero. The paired tunes in all three pairs differ in the very final portion of their f0 trajectories, with one tune rising to a slightly higher final f0 value than the other, paired tune. HHH and HHL show an additional region of difference in the shape and slope of the rise, with HHL having a shallower and slightly domed rise, and HHH having a steeper and more scooped rise. Notably, this difference in rise shape was not present in the model productions, where the f0 trajectories for these two tunes varied only in the region corresponding to the last syllable of the word, a distinction which is also reflected in Figure 10C.
Together, the GAMM analyses show fine-grained but detectable f0 differences between tunes that clustered together and were often misclassified for one another. These differences occur mostly in the very final portion of a final f0 rise, with one tune rising just a little higher than another tune with the same overall shape, and also in rise shape for the High-Rising tunes.
3.1.5. Turning point analysis
In the turning point analysis, we consider three tunes that are predicted to have f0 movements that rise from a low f0 target: LHH, LHL, and LLH (see Figure 1). The turning point timing model assessed the timing of the f0 minimum in the tune with respect to onset of the nuclear word. Based on the distinction in the f0 trajectories of the model tunes, we predicted a later f0 turning point for LLH compared with LHH and LHL, and no difference between LHH and LHL. With LHL set as the reference level in the model, we find a credible effect whereby the turning point is later in time for LLH (β = 25, 95CrI = [15,35], pd = 100). In comparison, LHH also shows credibly earlier alignment (β = –15, 95CrI = [–28,–1], pd = 98). We thus have evidence for a (small) alignment difference between these three tunes. Notably, the timing of the f0 turning point between LHL and LHH was not different in the model stimuli. The observed difference in the models is thus one that was created by speakers in their reproductions of the tunes, similar to the domed/scooped rise distinction evident in the GAMM modeling. We additionally note here that the empirical distributions of alignment timing across tunes are largely overlapping (see Figure 11); in this sense, there is clearly a large degree of within-tune variation in alignment, which entails substantial overlap across tunes.
3.1.6. Word duration analysis
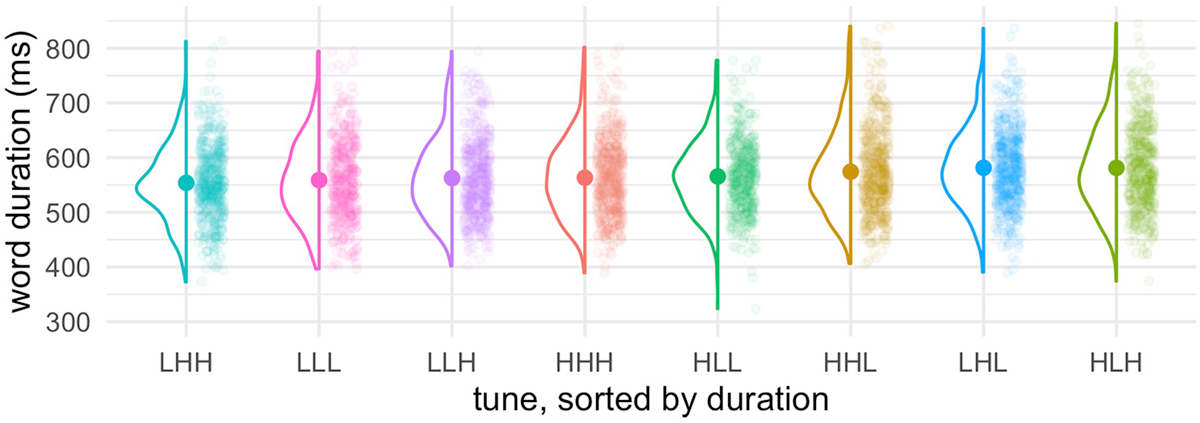
In the word duration analysis we consider how the duration of the nuclear accented word is impacted by tune and the nuclear accented word itself (Harmony, Madelyn, Melanie). We first consider the main effect of nuclear word, which showed a credible difference in overall duration (not shown). Extracting pairwise comparisons among the three nuclear words with emmeans (Lenth, 2021), we find that Madelyn is credibly longer than Harmony (β = 13, 95CrI = [–22, –3], pd = 99), and that Harmony is credibly longer than Melanie (β = 30, 95CrI = [20, 40], pd = 100; as is Madelyn: β = 43, 95CrI = [34, 51], pd = 100). Figure 12 shows the durational measurements by tune, sorted from shortest to longest mean tune duration. The model finds that there are additional small differences as a function of tune. The largest estimated difference, between LHH and HLH, is 26 ms. As can be seen in Figure 12, this is small when considering variation in duration distributions overall. Here we focus on the three confusable tune pairs, that were identified by the clustering analysis; a more complete summary of this data may be found online in the supplementary materials. There was a credible difference in duration between all three pairs: HHH vs. HHL (β = –9, 95CrI = [–17, –13], pd = 98), HLH vs. HLL (β = 13, 95CrI = [4, 23], pd = 100), LHL vs. LLH (β = 17, 95CrI = [7, 27], pd = 100). These differences are small (9–17 ms), representing approximately 1.5% to 3% of the mean word duration across all tunes (568 ms). Like the differences detected with the GAMM and turning point analysis, these durational differences constitute a possible (temporal) distinction among tunes, which in this case was not present in the model stimuli (for which all tunes were the same duration, for a given model word). This result, together with the turning point analysis, suggests that in addition to considering time-normalized trajectories (necessary for clustering, as we implemented by it), temporal properties of tunes may also constitute cues, though we reiterate that these differences are quite small in our data.
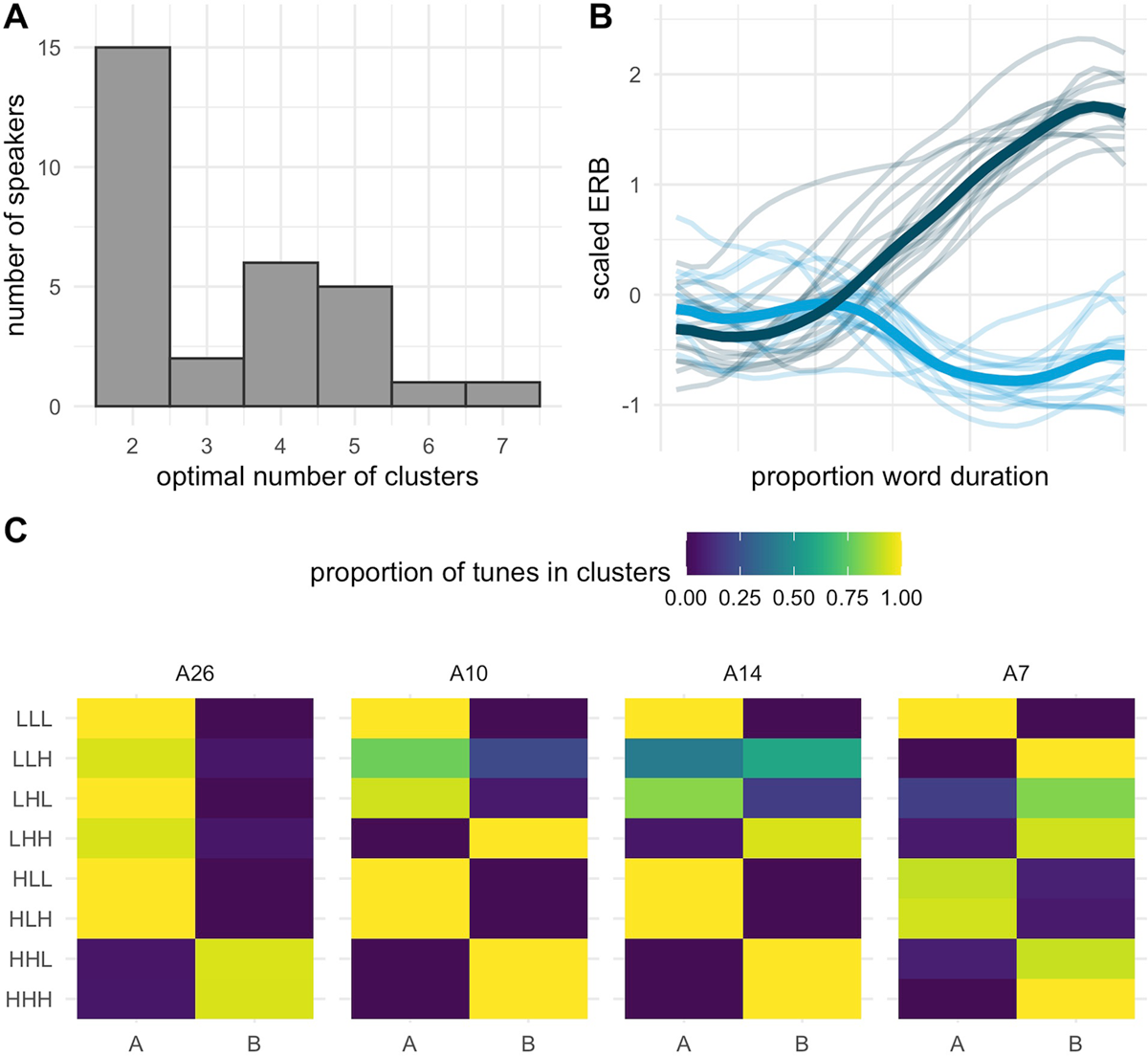
3.1.7. Individual-level clustering
The clustering analyses performed over individual participants reveals a range of variation in clustering solutions. As shown in Figure 13A, 15 participants produced f0 trajectories that were optimally grouped into only two clusters. Four participants produced a five-way cluster distinction, which roughly corresponds to the five-way distinction observed in the group-level clustering solution (Section 3.1.2). Six speakers evidenced a four-way distinction, which was again similar to the five-way group clustering solution, with the loss of one distinction (which varied by participant). Figure 13B shows the by-speaker cluster means for the 15 participants for whom two clusters was the optimal solution. The clusters that emerge for these two-cluster solutions can be generally characterized as rising versus non-rising, and this distinction, though implemented differently by participants, is a systematic difference between the clusters in the two-cluster solutions. Cluster means for all 30 speakers are shown in Figure A2 in the appendix.
Histogram showing the number of individual speakers who had a given number of clusters in their optimal solution (12A), by-speaker cluster means (light lines), and grand means (dark lines) for two cluster solutions for the 15 speakers for whom two was the optimal number of clusters, with the rising cluster in dark green, and the other cluster in light blue (12B), and clustering solutions for four example speakers for whom two was the optimal number of clusters (12C).
All but three of the 30 individual participants group the High-Rising tunes {HHH, HHL} into a single cluster. These are the same two tunes whose imitations formed Cluster C in the group level clustering analysis. Some individuals include other tunes with a rising shape {LHH, LHL, LLH} into this cluster. For the two participants whose productions of HHH and HHL were not grouped together into a single cluster, imitations of these tunes nevertheless showed very similar patterns of cluster assignment, with f0 trajectories for both tunes divided fairly evenly across two clusters. The pattern of incremental inclusion of additional tunes with HHH and HHL in the high-rising cluster is shown in Figure 13C, with heatmaps of the clustering solutions for four participants for whom the optimal number of clusters was two. At left is a speaker for whom HHH and HHL form a cluster to the exclusion of all other tunes. To the right is a participant who adds LHH to the high-rising cluster. The third heatmap is for a participant who contributes (some of) their LLH productions to the high-rising cluster. The rightmost participant groups HHH, HHL, LHH, LLH, and LHL together, with rising-falling HLL and HLH, and falling LLL in the other cluster. Table 2 additionally shows the graded and hierarchical nature of the clustering solutions across participants, counting the number of speakers who include other tunes with HHH and HHL, as shown by the examples in Figure 13B.
Counts of tune groupings across speakers in the individual clustering analyses. Note the second through fourth groupings are subsets of the first. “Mostly” is used to refer to a case when more than half of the productions of a given tune end up in a cluster.
| Grouping | # Participants |
| HHH and HHL cluster together in one High-Rising cluster (Figure 7b, participant A26) | 27 |
| LHH is also mostly in the High-Rising cluster (Figure 7b, participant A10) | 14 |
| LLH is also mostly in the High-Rising cluster (Figure 7b, participant A14) | 7 |
| LHL is also mostly in the High-Rising cluster (Figure 7b, participant A7) | 3 |
To summarize, the individual clustering analyses reveal a dichotomy between rising f0 trajectories that end in a high f0 and other trajectories that fall, or that have more complex shapes. This dichotomy is evident for all speakers, who vary only in which tunes map to the high-rising vs. “other” clusters. Some speakers produce additional fine-grained distinctions among tunes in the “other” clusters, though over half of the participants show only a two-cluster partition of the data. The individual clustering results thus complement the group-level analyses in showing (1) that participants vary in the distinctions they produce among nuclear tune imitations, and (2) that a singular distinction between a class of High-Rising tunes and other (Non-High-Rising) tunes is apparent for nearly all speakers. These findings point to a hierarchy of tune distinctions. There is a primary grouping, High-Rising vs. Non-High-Rising, with predictable membership of tunes in each group, and for some individual speakers, additional finer (or, secondary) distinctions, though for fully half of the speakers the optimal clustering solution yields only a two-way partition of the data. Clustering solutions for each of the 30 speakers are shown in the appendix (Figure A3).
3.2. Perceptual discrimination experiment
Given the data presented thus far, one outstanding question is the extent to which participants’ imitations are related to the perceptual distinctiveness of the tunes. Our focus in examining the perception results is accordingly to test if certain pairs of model tunes are discriminated at, or below, chance. We then consider how the patterns of perceptual discrimination relate to the grouping of tunes in the clustering solution and to the phonetic distance between model tunes.
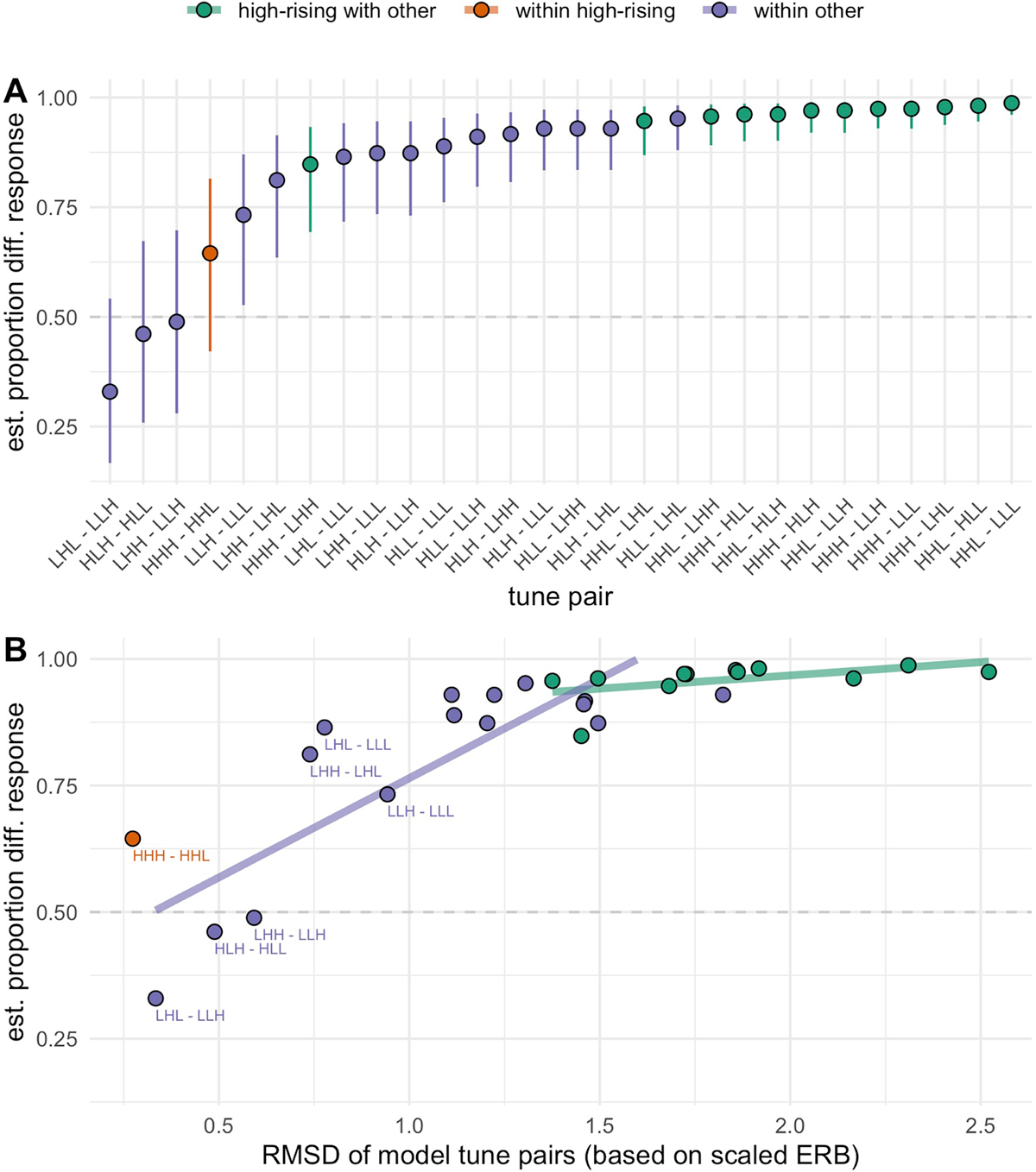
Figure 14A shows listeners’ perceptual discrimination of different tune pairs sorted from lowest (at bottom) to highest (at top). Points are colored by whether or not one tune in the pair is in the High-Rising set {HHH, HHL}. As shown in Figure 14A, accuracy varies across tune pairs, with four tune pairs discriminated at or below chance, as assessed by the CrI for the estimates including 0.50 (50% different responses). All other pairs are discriminated above chance, though with a range of accuracies. Three of the four pairs discriminated at or below chance are the same pairs that were grouped together in the group-level clustering analysis: {LHL, LLH} formed Cluster A, {HLH, HLL} formed Cluster B, and {HHH, HHL} formed Cluster C. The same three pairs were also frequently confused by the neural net classifier. One additional tune pair, {LHH, LLH}, was also poorly discriminated. Notably, in the group-level clustering analysis, this pair was fairly well distinguished, with LHH primarily contributing to Cluster D, and LLH contributing to Cluster A. However, the neural net classification notably showed a high rate of confusions for this pair and the three other pairs mentioned above, evidencing a parallelism between listeners’ perceptual responses and the classification of imitations.
Speech perception experiment results, with Panel A showing the estimated proportion of correct “different” responses as a function of tune pair, sorted from least to most accurate. Error bars show 95% credible intervals from the model fit. Coloration indicates whether a tune pair includes a High-Rising tune (HHH or HHL). Panel B shows the same data on the y-axis, as a function of pairwise distance (RMSD) on the x-axis. Two separate regression lines are fit, based on whether tune pairs include high-rising tunes compared with other tunes, or other tunes compared with one another.
Next, consider the relationship between discrimination accuracy and whether or not one tune in the pair contained a member of the High-Rising class {HHH, HHL}, indicated by color in Figure 14. As shown in analyses of the production data, imitated productions of these two tunes cluster together and are frequently confused for one another in classification, but in both analyses, these two tunes are well distinguished from all others. Most notably, in the individual clustering analysis, it was shown that almost all speakers grouped these two tunes together in a High-Rising cluster, which for some individuals also included other tunes with rising shapes. The perception data echoes this finding in showing that for pairs that include a High-Rising tune, either HHH or HHL, paired with a tune not from the High-Rising class, discrimination is high (e.g., the nine tune pairs with the highest discrimination accuracy are of this type). The only tune pair of this type without near-ceiling discrimination is HHH and LHH, and it is relevant to recall that LHH was the tune most frequently added to the High-Rising cluster in the individual clustering analyses, for individuals who expanded that cluster to include three tunes (Section 3.2.2).
Figure 14B shows how discrimination accuracy relates to the phonetic distance between two tunes in f0 space, computed for the model tunes using the distance measure (RMSD) as described in Section 2. At first glance, a larger distance between two model tunes corresponds to higher discrimination accuracy. The purple line in Figure 14B indicates the linear regression fit for tune pairs that combine tunes from the “other” (Non-High-Rising) class, showing a positive correlation: The distance between model tunes in f0 space is a good predictor of their perceptual discrimination. For pairs that combine a High-Rising tune with a Non-High-Rising tune from the “other” class, there is a weaker positive correlation, shown by the green line, though in this case there is little variation in perceptual discrimination against a much larger range of variation in f0 space. In other words, when one member of a tune pair is HHL or HHH, discrimination accuracy is not only high, but is based less directly on the phonetic details of the stimuli. This can be taken as converging evidence for the status of the High-Rising tunes as the basis of a contrastive High-Rising tune category, which is well discriminated with respect to other tunes.
4. Discussion
The present study examined the extent to which the predicted eight-way distinction in nuclear tune shape, as posited in the AM model of American English intonation, was reliably reproduced in an imitative speech task and if the same set of tunes were reliably discriminated in a speech perception task, by L1 speakers of American English. We first discuss evidence that validates the imitation task as involving a transduction of tunes from perception to production, by which an auditory model tune is encoded in terms of its salient features, which may not, however, precisely replicate the phonetic detail of the model tunes. We then discuss the production and perception findings as they bear on the question of the number and type of distinctions among tunes. We further note that the reader can use an interactive shiny app to explore some parts of the data presented in this paper, which may be found at https://prosodylab.shinyapps.io/nuctunes-basic8/.
4.1. Evidence that imitation is not parroting
From the accuracy results we establish that the imitation task involves a transduction of the f0 trajectory of the (heard) model tune onto the f0 trajectory of an imitated production that captures the shape-based distinctions between tunes, but which does not amount to a simple parroting of the auditory stimulus. This claim is supported by the observation that imitations following the male model speaker are more accurate with respect to the model than are imitations following the female model speaker, for male and female participants alike. If imitations were produced with the goal of reproducing the phonetic detail of the heard tune (in a parroting fashion), we would expect differences in accuracy based on the match between the gender of the model speaker and the participant, rather than across-the-board higher accuracy for imitations following the male model speaker. The lower accuracy following the female model speaker results from the apparent reluctance on the part of our participants to match the female speaker’s larger pitch range, and in particular the higher f0 targets in her range. Further evidence that imitations were non-exact reproductions of the models comes from the observation that the imitated tune productions did not show the same patterns of separation in f0 space as observed for the models. That is, participants did not match their productions to the models in terms of the distance between pairs of tunes. Moreover, these differences between the pairwise distance measures of model tunes vs. participants’ productions were not uniform, showing that while some tune pairs were reproduced in a way that preserved the pairwise distance in model tunes, other tunes were not (as shown in Figure 4).
Finally, imitations introduce certain features that were not present in the auditory models, specifically, a distinction between a scooped shape of the accentual rise for HHH and LHH tunes, which is distinct from the domed shape for HHL. These results confirm that in using an imitative speech production task, we are eliciting tune productions that reflect the participant’s encoding of a heard tune in a form that captures salient distinctions in tune shape, preserving relative but not absolute scaling of (at least some) tonal targets.
4.2. Number and shape of emergent tune classes
Using clustering and classification analyses, we asked if each of the eight tunes is robustly distinct from the others, as predicted by the eight-way phonological contrast of the AM model. Clustering analyses over unlabeled f0 trajectories offer support for only five distinct tunes, whose f0 trajectories can be characterized as low-to-mid rising (Cluster A), rising-falling (Cluster B), high-rising (Cluster C), low-to-high rising (Cluster D), and low-falling (Cluster E). Results from neural net classification of the same imitated f0 trajectories suggest a similar partition of the data, where the tune pairs that are most confusable for the classifier are those that are grouped together in the clustering analysis. Separate clustering analyses over individual participants’ data further complements these results, identifying some tune distinctions as more robust than others. In particular, the clustering solutions for 27 out of 30 participants group the High-Rising tunes {HHH, HHL} together into a single cluster, which for some participants may also include imitations of other tunes with rising shapes, namely LHH, LLH, and LHL (in order of increasing likelihood of inclusion based on the number of participants who include other tunes in the High-Rising cluster).
Taking the clustering and classification results together, we have evidence that supports a five-way distinction among tunes, with a hierarchical ordering of tunes in at least two levels. First, there is a primary distinction between a High-Rising and Non-High-Rising class, which are the most separable tune classes in the clustering and classification analyses and are grounded in distinctions in the distance between tunes and tune clusters in f0 space. Second, the High-Rising vs. Non-High-Rising distinction is the single most common distinction in the clustering solutions, observed in the clustering solution for the vast majority of individual participants.12 There is also evidence for less robust, secondary distinctions among the Non-High-Rising class, which are observed in the group-level clustering analyses but not consistently in the analyses of individual participants. Distinctions among tunes in the Non-High-Rising class are also less accurately discriminated in the classification analysis, especially between tunes that cluster together in the group-level clustering solution. The hierarchical ordering of tunes is explicit in the clustering diagram based on output from the neural net classifier (Figure 7B).
Despite evidence of the apparent loss of predicted tune distinctions from the clustering and classification analyses, the GAMM and f0 turning point analyses suggest that within the emergent tune classes the “lost” tune distinctions are detectable in more fine-grained acoustic analyses using labeled data (i.e., comparing imitated f0 trajectories identified by the label of the model tune being imitated). The GAMM analysis in particular shows that the tune pairs that cluster together and are often misclassified for one another nonetheless exhibit small differences in some regions of their time-normalized f0 trajectories. The GAMM difference smooth for the pair of High-Rising tunes {HHH, HHL} reveals a domed vs. scooped distinction in rise shape. In addition, the difference smooths for all three of the collapsed/confusable pairs shows a distinction in the ending f0 values that reflects the same distinction in final f0 of the model tunes. The f0 turning point analysis suggests an additional, though small, distinction in the alignment of the f0 minimum (the rise onset) between three tunes that rise from an initial low target: {LHH, LHL, LLH}. The latter two, {LHL, LLH}, clustered together in the group-level analysis and tended to cluster together in the clustering solutions of individual participants. These findings from GAMM and f0 turning point analyses point to structured variation within the emergent tune classes, which, however, was only apparent when we examined data with reference to the label of the model tune that was the target of imitation (i.e., with labeled data).
The perception data align with analyses of the speech production data in the sense that tunes that are poorly discriminated in perception tend to be those that (1) cluster together, (2) are confusable in classification, and (3) have only relatively small differences in their f0 trajectories as detected by GAMM and f0 turning point analyses.
4.3. Relating phonetic distance, perceptual discrimination, and distinctions in imitated tune production
Here we consider how the emergent tune distinctions from the production data relate to the acoustic and perceptual distinctiveness of the model tunes, and how the acoustic and perceptual distinctions relate to one another. The aim of this discussion is to determine the extent to which the perceptual salience of tunes explains the number and nature of the distinctions produced in their imitation. Specifically, we ask if the perceptual discriminability of the model tunes, grounded in their phonetic differentiation in f0 space, explains variation in the accuracy of the imitations. We begin by assessing the phonetic distance between pairs of model tunes in relation to their perceptual discrimination. We next compare variation in the phonetic distance between pairs of model tunes to the clustering and classification analyses of the imitation data. Seeing that the phonetic differentiation of model tunes does not fully explain variation in the perception and production data, we turn to examine how the perceptual discrimination of model tunes relates to the distinctions that emerge in the production data. We will argue that asymmetries between these measures offer further support for the hierarchical ordering of tunes, which does not reduce to phonetic distance, with a primary distinction between High-Rising and Non-High-Rising tune classes, and secondary distinctions among other tunes.
4.3.1. Relating phonetic distance to perceptual discrimination
As shown in Figure 14B, the distance in f0 space between pairs of model tunes, measured in terms of RMSD, varies in relation to their perceptual discrimination. Yet phonetic distance does not fully explain perceptual discriminability. Consider the seven most similar pairs of model tunes (i.e., the ones that are the closest to one another in f0 space; in Figure 14B, the pairs with values below 1.0 on the x-axis). Among these pairs of phonetically similar tunes, there is striking variation in perceptual discrimination accuracy, with three pairs discriminated at or below chance (0.50), and the other pairs discriminated with model estimated accuracy ranging from 0.65 to 0.85. Notably, the tune pair with the lowest distance, {HHH, HHL}, is discriminated well above chance, with accuracy comparable to that of tune pairs with much greater distance.
Turning now to the tune pairs with the greatest distance, the relationship between discrimination and distance is different depending on whether the tune pair includes one of the High-Rising tunes {HHH, HHL}. For tune pairs in which only one tune is from the High-Rising class, perceptual discrimination is near ceiling, and there is relatively little improvement in discrimination as a function of increasing distance (green data points in Figure 13B). For tune pairs that do not include a member of the High-Rising class, a greater distance boosts perceptual discrimination, which for this set ranges from poor (below chance) to near ceiling (purple data points in Figure 14B). What we see is that perceptual discrimination performance is warped by tune class: When tunes differ from one another in a particular way they are better distinguished perceptually, and the key perceptual criterion is the distinction between High-Rising and Non-High-Rising tune classes.
4.3.2. Relating phonetic distance to distinctions in imitated tune production
The phonetic distance between model tunes provides a similarly incomplete account of the speech production data. Consider again the seven tune pairs with the smallest distance (RMSD < 1). Three of these tune pairs also fail to be distinguished in the group-level clustering analysis of imitations: {HHH, HHL}, {LHL, LLH}, {HLH, HLL}. But for two other tune pairs with small distance, the paired tunes are distinguished in clustering—they do not cluster together. For example, LHH and LLH are relatively close in f0 space, being the fourth lowest tune pair in terms of phonetic distance. This pair is also poorly discriminated in perception, and yet these two tunes cluster separately in the group level analysis, with 93% of LHH tokens grouped in the low-to-high rising cluster (Figure 5, Cluster D), and 97% of LLH grouped in the low-to-mid rising cluster (Cluster A). Similarly, LHH and LHL cluster separately but are the fifth lowest pair in terms of phonetic distance (this pair fares better in perceptual discrimination, with above chance accuracy). In short, for tunes that are very similar in f0 space, phonetic distance does not go far in predicting clustering outcomes. Looking at tune pairs that are more dissimilar in f0 space (RMSD > 1), we find only a weak relationship between phonetic distance and the clustering of imitations. Notably, while the phonetic distance measure varies continuously across this subset of the data, with distance RMSD values between 1 and 2.5, the clustering analysis points to a more discrete partition of the tunes. Imitations of tunes in the High-Rising class are reliably clustered separately from productions of other tune classes, regardless of the phonetic distance between the High-Rising tune and the other Non-High-Rising tune. Put differently, a decrease in phonetic distance for such tune pairs (the green data points in Figure 11B) does not predict a higher proportion of either tune clustering with the other. Relating phonetic distance to accuracy of neural net classification of tune pairs leads to a similar conclusion: The difference in confusion rates across tune pairs does not mirror the more continuous variation in phonetic distance.
To summarize, model tune pairs exhibit variation in phonetic distance across a broad range of RMSD values. Perceptual discrimination of the same tune pairs varies from below-chance to ceiling accuracy, with most tune pairs discriminated well above chance. If distance and discrimination accuracy, as measures of the distinctiveness of model tunes, were the main factors driving tune imitations, we would expect to see correspondingly gradient variation in imitations in terms of how they cluster (i.e., in the proportion of imitations of two tunes that are assigned to same cluster) and in classification accuracy (pairwise confusion rates). Instead, the clustering and classification results point to a more discrete partition of tune imitations into two robustly distinct primary classes, High-Rising and Non-High-Rising, with up to four additional classes within the Non-High-Rising set that emerge for productions aggregated over individuals. Tunes grouped together into any one of these five classes tend to cluster together and be confused for one another in classification, while tunes from different classes tend to cluster separately and are rarely confused with one another, especially for tunes across the High-Rising/Non-High-Rising divide.
4.3.3. Relating perceptual discrimination to distinctions in imitated tune production
We have asked whether phonetic distance by itself can explain variation in our perception and production data, because of the reasonable belief that if listeners cannot perceive subtle f0 distinctions between two tunes then they will not be able to reproduce those distinctions when imitating the tunes from auditory models. At the same time, our test of perceptual distinctions among tunes is based on listeners’ explicit judgments in an AX discrimination task. We acknowledge that AX discrimination is a metalinguistic judgment that may not fully reflect listeners’ perception of the auditory signal. For instance, a listener may perceive a subtle distinction in f0 between two auditory models yet judge that distinction to be below the threshold for declaring the tunes to be different. This scenario could arise if a listener perceives an f0 distinction between a pair of stimuli as within, rather than between-category variation for the category distinction they invoke in making the same/different judgment. If we allow that within-category phonetic variation may be specified in the encoding of a heard tune, just as evidence suggests it is for segmental categories, it follows that a participant may subsequently reproduce that phonetic detail in their imitation of the tune. This could occur even if the participant does not reliably discriminate tunes on the basis of the same phonetic detail in the AX perception task. In that scenario, a participant may hear phonetic detail that does not bear on their same/different judgment for the AX task, but which may be reflected in their imitations. A finding of this sort would shed light on the f0 properties of tunes that are represented as targets for production, and those properties that serve to make categorical same/different judgments. To explore this question, we directly compare the perceptual discrimination results for specific tune pairs with analyses of the production data for the same tunes. There are three relevant observations:
First is the straightforward observation that the neural net classifier trained on the model tunes succeeded in classifying imitations according to the label of the corresponding model tune with accuracy well above chance (Figure 6, values on the diagonal; chance = 12.5%). Confusions were high for the four tune pairs with the lowest accuracy in perceptual discrimination {LHL, LLH}, {HLH, HLL}, {LHH, LLH}, and {HHH, HHL}, but classification was still well above chance, indicating that the neural network was able to find information in the imitated f0 trajectories (specified by f0 and Δf0 at each time step) that distinguishes each tune as distinct from other tunes, to some degree. The above-chance performance of the classifier is clear evidence that participants implemented measurable f0 distinctions among tunes, however small or inconsistent they may appear.
A second observation related to the same four poorly discriminated tune pairs is that small f0 distinctions between tunes in these pairs were evident in the GAMM estimates (computed from the difference smooth GAMM, Figure 9A), in small but significant differences in their f0 trajectories. Except for the pair {LHH, LLH}, these small f0 differences in the imitated tunes were not sufficient as the basis for a clustering distinction, and the corresponding f0 differences of the model tunes were not sufficient as cues for perceptual discrimination (compared with other tune pairs). Similar evidence comes from the turning point analysis, where small differences in the location of the accentual rise onset were significant among the three tunes {LHL, LLH, LHH}, yet were not sufficient cues for perceptual discrimination.
A third observation concerns the asymmetry between perceptual discrimination of model tunes and clustering of the corresponding imitations, for some tune pairs. For example, the tunes {LLH, LLL} are robustly distinguished in the clustering analysis of group data (from Figure 5B: Only 3% of LLL imitations cluster with LLH, and no LLH imitations cluster with LLL), yet the corresponding model tunes are the fifth lowest in discrimination accuracy (Figure 13A: Below 75% accuracy). Similarly, {LHH, LLH} rarely cluster together in the group data (only 7% of LHH imitations cluster with LLH, and only 3% of LLH imitations cluster with LHH), yet they are the sixth lowest tune pair in discrimination accuracy, at 80%. On the other hand, for the pair {HHH, HHL}, discrimination accuracy is well above chance at 62%, and yet these tunes are never distinguished in imitations. Without exception, imitations of HHH and HHL cluster together in the clustering solutions of both the group and individual data.
These examples demonstrate that a distinction between two tunes in production does not necessarily correspond to a perceptual distinction of comparable strength. The implication is that some f0 features of the model tunes may be represented as targets for imitation, yet do not serve as strong cues for a same/different judgment in the AX task. In the case of {LHH, LLH}, the small f0 distinction between the model tunes gives rise to a moderately robust distinction in production as the basis for grouping imitations of these two tunes in different clusters. For {LHL, LLH}, {HLH, HLL}, {HHH, HHL}, the f0 features distinguishing the paired tunes are revealed only at the level of fine-grained acoustic analysis. All these cases provide evidence that some f0 distinctions are perceived and encoded, yet do not qualify as cues for a categorical same/difference judgment.
4.3.4. Summary: A High-Rising/Non-High-Rising dichotomy
To sum up this section, the findings from analyses of phonetic distance, perceptual discrimination, and distinctions among imitated tunes point to a primary partition of the eight nuclear tunes into two classes: High-Rising and Non-High-Rising, with five emergent categories within this primary dichotomous distinction. The individual clustering analyses show that there is variation among speakers in how the primary partition is achieved, allowing for a more (or less) strict criterion for the inclusion of tunes other than {HHH, HHL} in the High-Rising class. When comparing model tunes across the High-Rising/Non-High-Rising division, phonetic distance is greatest and perceptual discrimination is near ceiling. For the imitated tune productions, a distinction across this division is the sole distinction we consistently observe across individual participants. Our findings support an analysis of the primary High-Rising/Non-High-Rising distinction as categorical. Alternatively, the variability within each category suggests a characterization in terms of two attractor tunes, as proposed by Roessig, Mücke, and Grice (2019), which are maximally distinct in f0 space and exert an especially strong force in perceptual discrimination, and which also characterize variation in production. Variation around the High-Rising and Non-High-Rising attractors results in smaller, less salient f0 distinctions, which less reliably cue a categorical same/different judgment and are less reliably implemented in tune imitation. The proposed hierarchical organization is shown in Figure 15 (tone labels on nodes corresponding to emergent clusters are discussed in the next section).
4.4. Relating emergent clusters to proposed distinctions of the AM model
Our motivation in examining the f0 trajectories of imitated tunes was to test the predictions from the AM model about the realization of phonological contrasts resulting from the concatenation of a monotonal pitch accent, phrase accent, and boundary tone. One view of the data is thus to ask how these phonological contrasts relate to the distinctions evident in our imitation data. In the group-level clustering analysis, tunes with different pitch accents (H*, L*) are grouped into different clusters (Figure 5B). Clusters A and C include imitations of tunes with H* accents; these are the Rise-falling and High-rising groups in Figure 14. Clusters B, D, and E contain imitations of tunes with L* accents: The Low-falling, Low-to-mid and Low-to-high groups in Figure 14. In comparison, phrase accent and boundary tone differences are not clearly reflected in clustering. For tunes that cluster together, the pair {LLH, LHL} differ in both phrase accent and boundary tone, {HLH, HLL} differ in phrase accent, and {HHL, HHH} differ in boundary tone. In that sense, the results support a categorical partition of tunes based on a distinction between L* and H* pitch accents, which are well differentiated from one another in all four contexts of a following phrase accent and boundary tone: {H-H%, H-L%, L-L%, L-L%}. Note, however, that the partition of tunes based on pitch accent does not align with our results, pointing to a primary partition of tunes into a High-Rising and Non-High-Rising class. Further, the clustering analysis does not reveal a partition of the tune set based on either the phrase accent or boundary tone, considered independently; this is clear in observing the groupings of the tunes in relation to tune labels from the AM model (at right in Figure 14). Therefore, our imitated tune data do not support a model of tune contrasts defined over all three phonological dimensions as proposed in the AM model. In particular, the phonological contrasts that are phonetically implemented through small differences in the alignment of f0 turning points or in ending f0 values of a tune are not reliably captured in our data.
What then, do the present data suggest for a theory of intonational phonology? Most fundamentally, as described above, they suggest that tunes should not be viewed as unrelated or unorganized phonological entities, but rather as hierarchically ordered, where one distinction in particular, the High-Rising/Non-High-Rising distinction, is privileged, in the sense that it is more consistently differentiated in production across individual speakers, and more robustly discriminated in perception.
In a first approximation, we can describe the differences in the mean f0 trajectories of the emergent clusters, as shown in Figure 5A, in terms of an initial distinction corresponding to the pitch accent (H* or L*), and a three-way distinction in the final f0 target (high, mid, low: Labelled as H%, M%, and L% in Figure 12). Combinations of these two parameters (though not all combinations, there being no H*M%) yield the five emergent tune clusters, as indicated in Figure 12. However, these two dimensions alone do not fully capture differences in the shape of the f0 trajectories. For example, the Low-to-high rising tune shape (Cluster D from the k-means analysis) differs from the Low-to-mid rising tune (Cluster A), not only in terms of the f0 values at the end of the tune, but also in the slope of the rise from the initial low and the shape of the elbow in the tune. These observations merit a more holistic consideration of f0 trajectories in the nuclear region, considering how tune shapes, as revealed in their f0 implementations, differ from one another across the entire tune.
There is additional evidence for shape-based distinctions among tunes in the imitations of tunes with a rising shape. For instance, the mean f0 trajectory of Cluster D (Figure 5B), with a low-to-high rising shape, has a clearly scooped rise, while the mean f0 trajectory of Cluster C, with a high-rising shape, is more domed in shape. A similar distinction is observed within Cluster C, comparing imitations of HHH and HHL. In the GAMM analysis, HHH differs from HHL in having both a more scooped rise, and a higher ending f0 value (see Figure 8C). Notably, this difference is present in the region of the pitch accent, which in both tunes is H* (followed by H- in both tunes as well). To the extent that the AM model predicts that the shape of trajectories should result from interpolation between f0 targets, this sort of shape distinction is not predicted or well explained. An alternative account for shape distinctions is proposed in the Tonal Center of Gravity model (Barnes, Veilleux, Brugos, & Shattuck-Hufnagel, 2012; Barnes, Brugos, Veilleux, & Shattuck-Hufnagel, 2021), where variation in the shape of f0 rises (and falls) serves to displace the perceptually significant “center of gravity” for an f0 movement within a certain temporal interval. A domed rise corresponds to an earlier center of gravity, while a scooped rise corresponds to a later one. Our findings suggest that such distinctions may be pertinent in nuclear tunes with a rising shape, whereas previous literature has focused on the center of gravity of rising-falling shapes that arise in the implementation of a pitch accent alone (disregarding the following intonational context). The scooped-dome distinction observed in our data among tunes with a rising shape is at odds with a strict target-and-interpolation view of f0 in intonation systems, as proposed in the AM model.
4.5. Limitations of this study and future directions
Although the findings of this study are clear and compelling, with converging evidence showing a hierarchical grouping of the eight basic nuclear tunes posited by AM theory, a number of issues may limit the conclusions that can be drawn and suggest avenues for additional studies to explore the generalizability of the results. In this section we discuss limitations concerning how our tune stimuli were created and the absence of discourse context in the experimental task, pointing to areas where additional empirical data and future methodological advances are called for.
First, the bedrock assumption of the experiments reported here is that the resynthesized versions of the tunes that served as stimuli capture the essential properties of the f0 trajectories that adequately distinguish the proposed eight basic nuclear tunes. To the extent that this is true, these experiments provide a searching test of how speakers and listeners treat these tunes. However, if the resynthesized f0 trajectories are not adequate representations of the basic tunes, and in particular if some stimulus tunes were better representatives of their category than others, then it may be the case that the stimuli that were less accurately imitated and less categorically perceived are those which less adequately represented their categories. As described earlier, our resynthesis method was informed by the schematized rendering of f0 targets for the three tonal components of the tune, following the online ToBI training materials and the f0 tracings from natural productions in Pierrehumbert (1980). These materials do not specify precise phonological or phonetic landmarks for the alignment of f0 targets. In the absence of community-endorsed guidelines, we relied on our collective experience with ToBI labeling of American English to identify phonological landmarks as anchors for each tone, which were then systematically used for all tunes and all model sentences. Nonetheless, despite our best efforts, it is possible that the resynthesis was more successful for some tunes than for others and that our results were influenced by such differences. A superior resynthesis method would have been informed by natural productions of the eight tunes by the same speaker, for many speakers of the same dialect, but to date no such dataset exists.13
Another possibility is that our resynthesis method omitted some cues that play a critical role in the perceptual discrimination of tunes. It is possible that speakers/listeners differ in the weights they place on different cues, or that they have different habitual acoustic-phonetic implementations of a given target contour, and any such differences could be a source of the individual differences observed in the clustering analysis of our data. For instance, the eight stimulus tunes used here were distinguished only in their f0 trajectories; if natural productions include additional cues to contrasts among the tunes, related to e.g., duration, amplitude, or voice quality, these cues were not implemented in the experimental stimuli. Implementing additional cues to intonational contrasts remains a goal for future research. More empirical data is needed to inform these future directions.
A further limitation of our stimuli is that the preambles for each of the eight tunes were identical; if natural productions include some cues located in the preamble, these cues were missing from the stimulus contours.14 It is not entirely clear how to address these issues about tune resynthesis experimentally, but the results presented here provide an initial set of findings that can guide such future research.
A second limitation concerns the phonological restrictions we imposed on the sentences our participants produced. The nuclear tune was always produced over a three-syllable word with initial stress, in which all but the word-initial consonant was voiced. While these restrictions reduced errors in f0 tracking and facilitated pooling data across the three target words, they do not allow us to see whether or how speakers modify an f0 trajectory to accommodate a shorter or longer nuclear tune interval, or voiceless consonants within that interval. Prior studies on intonation production show substantial variation related to such phonological factors, with evidence of truncation and compression effects in shorter intervals (e.g., Arvaniti et al., 2007; Grabe et al., 2000), variable alignment of a phrase accent depending on the syllable and stress pattern following the nuclear accented syllable (Grice, Ladd & Arvaniti, 2000), and effects of segmental voicing on the realization of intonational features (Roettger & Grice, 2019). Examining tune imitations in more varied phonological contexts is a focus of our ongoing work.
A third limitation of this study is that in both the production and AX perception experiments, nuclear tunes were presented to participants in the absence of a discourse context. This paradigm allowed us to test the reliability and robustness of hypothesized contrasts that can be a priori distinguished independent of context. However, to the extent that the production and perception of a given tune may be facilitated in a particular discourse context, the present results cannot speak to the system of tune distinctions available when supported by contextual information. The absence of discourse context is a limitation of our study, but one that was motivated on two grounds. First, on analogy with segmental phonology, we reasoned that a phonological contrast between two intonational forms should be accessible without contextual support, both in production and perception. We acknowledge that a contrast may be restricted to certain phonological contexts, as attested for segmental contrasts, but looking across a range of contexts, we expect that a given phonological contrast will be phonetically implemented in at least some of them. We examined proposed distinctions between monotonal pitch accents {H*, L*}, phrase accents {H-, L-} and boundary tones {H%, L%} in all their combinations, which (excluding additional pitch accents and the influence of preceding context) exhausts their combinatorial possibilities. Any loss of a predicted contrast among the eight tunes we tested therefore presents a serious challenge for the proposed underlying phonological specification. The second reason for omitting discourse context in this study is a practical one, already mentioned in Section 1, and that is that work on intonational meaning in American English has not yet identified a clear pragmatic function for many of the nuclear tunes tested here, and even for those tunes that have been studied, the existing work has not converged on a pragmatic framework that could easily be extended to all tunes. This gap in our understanding makes the design of experiments to test the effect of discourse context challenging.
Since our participants were not given an explicit discourse context to guide tune interpretation, they may have inferred tune meaning, and therefore any effect of context on tune production or perception is an uncontrolled factor in our study. Our study documents a set of up to five distinct tunes which, based on their phonetic and phonological substance, are accessible in production and perception in the absence of a specified discourse context. An important future direction for research on American English intonation will be to test the distinctions among the eight basic nuclear tunes of AM theory (as well as other tunes) when they are situated in a discourse context with pragmatic conditions that facilitate the production of a given tune (and perhaps even in contexts which are not appropriate for the tune, to examine its robustness). If it is the case that some distinctions are more robust in a supportive discourse context (e.g., HLL and HLH, which are not well distinguished in our data), this would be added support for the notion of a hierarchy of tune distinctions, where the most robust distinctions are context-independent and finer distinctions (e.g., those evident in the GAMM modeling) are accessed only with contextual support. Future work along these lines will help us to develop a comprehensive model of intonational distinctions as produced and perceived by speakers.
5. Conclusions
The present study takes a first step in understanding the system of distinctions among the melodies in the nuclear region of the intonational phrase in American English, relating distinctions in the imitation of tunes to distinctions in phonetic distance and perceptual discriminability. The evidence presented here suggests that some of the distinctions proposed in the AM model are lost or have diminished status for most speakers. Taking a birds-eye view of our findings, we have converging evidence from analyses of phonetic distance, perceptual discrimination, and distinctiveness in production that favors a hierarchy of tune distinctions in this sense. The most robust distinction is between a class of High-Rising and Non-High-Rising tunes, though this can be achieved in various ways by individual speakers adopting more or less strict criteria for inclusion in the High-Rising class. Beyond this primary distinction, there is evidence for five emergent tune classes, and further evidence for structured variation within classes that reflects additional tune distinctions of the AM model, though these are implemented less reliably and by small f0 measures. Fine-grained variation within emergent tune classes is observed in the height of the final f0 and in a systematic distinction between tunes with a domed vs. scooped f0 rise. The distinction in rise shape, observed in two of the five tune categories in our data, is not predicted by target-and-interpolation models such as AM, and calls for alternative approaches that model intonational contrast in terms of dynamic, non-linear f0 trajectories.
The AM model predicts three pairwise distinctions among tunes that are not observed in our clustering or perception data. While the lost distinctions are between tunes that are very similar in f0 space, a comparison of phonetic distance, perceptual discrimination, and distinctions in tune production for all tune pairs weighs against a reductionist account that explains the lost distinctions as resulting from participants’ failure to perceive small f0 distinctions in the model tunes in our imitation task. We argue that the phonetic distance and perceptual discrimination results are better described in terms of the primary distinction between High-Rising and Non-High-Rising which function as attractors in the landscape of variable f0 trajectories. Phonetic distance and perceptual discrimination are very robust between these attractors, much more than for distinctions that are on the same side of the attractor divide.
The findings from this study have implications for the AM model for American English, in which nuclear tunes are defined by the concatenation of pitch accent, phrase accent and boundary tone. Our findings support a contrast between tunes with high- vs. low-tone pitch accents (H*, L*), which are robustly distinguished in perception and are reliably produced by nearly all speakers in this study. Secondary distinctions, less robust in our data, are best characterized in terms of a binary (H%, L%) or at most ternary (H%, M%, L%) contrast in boundary tone. Our findings do not support a tune contrast based on phrase accent (H-, L-) alone or in combination with boundary tones.
Finally, this study tests the distinctiveness of American English nuclear tunes in utterances produced and perceived in the absence of discourse context. While our findings provide clear evidence that tunes with a high-rising f0 trajectory are representationally distinct from other tunes, independent of context, other distinctions in tune shape are less reliably and consistently expressed in our data. Anecdotal descriptions of these “lesser” tunes (and others) that appear in the literature (e.g., Bolinger, 1986; Pierrehumbert & Hirschberg, 1990; see review in Westera et al., 2020) typically invoke discourse contexts, sometimes richly specified, raising the possibility that salient context is a necessary condition for accessing finer tune contrasts in speech production and perception. Beyond the work presented here, a more complete understanding of nuclear tunes in American English requires consideration of proposed pitch accent contrasts not included in this study (i.e., the bitonal and downstepped-high pitch accents), and integrated analyses of the multivariate, dynamic phonetic form of tunes and their pragmatic meaning.
Appendix
NN classification accuracy for a variety of input representations. The error bars indicated plus and minus 2 standard deviations for each input. The parameters which are varied are of (1) time-normalized vs. raw-time measurements (labeled as normalized/unnormalized) (2) f0 estimates in (speaker-centered) Hz or ERB units (cf0/cerb in plot); (3) f0 estimates at each sample x, the difference between x and the following sample (dx), or both (x & dx), and (4) the whole utterance (sent), just the preamble (pre), or just the nuclear word (nuc).
Cluster means for each speaker, sorted by the number of clusters. The label for each panel is the number of clusters followed by the speaker id number (A1–A30). For two-cluster speakers, labels have been standardized so that Cluster B is always the rising cluster, but for other speakers, cluster labels are arbitrary (compare to Figure A3).
Heat maps for each of the 30 speakers in the speech production experiment, showing the optimal clustering solution, with clusters in columns and tunes in rows. The label for each panel is the number of clusters followed by the speaker id number (A1–A30). For two-cluster speakers labels have been standardized so that Cluster B is always the rising cluster, but for other speakers cluster labels are arbitrary (compare to Figure A2).
Notes
- See Ladd (2008) for a review and discussion of the pitch accent inventory for American English proposed by Pierrehumbert (1980) with subsequent modifications in later works by various authors. [^]
- These findings from studies of intonation imitation have a parallel in studies that report within-category imitation of acoustic correlates of segmental contrasts, including stop voicing, vowel place, and nasality (Nielsen, 2011; Babel, 2012; Zellou, Scarborough & Nielsen, 2016). [^]
- This does not entail that a nuclear tune shape is necessarily a gestalt category, or smallest unit of analysis. A tune category may have internal structure, being composed of smaller internal units as with H and L tones in the AM model. [^]
- Pierrehumbert and Hirschberg propose a compositional theory of intonational meaning, where the meaning of a tune derives compositionally from the meaning encoded by each component feature: Pitch accent, phrase accent, boundary tone, in their tonal specification (e.g., as H or L). [^]
- All scripts and data for the experiment, including audio data for the model stimuli and participants, can be found on the OSF at https://osf.io/zgvnp/. An interactive webpage that can be used to explore some aspects of the data is also available at https://prosodylab.shinyapps.io/nuctunes-basic8/. [^]
- We also computed distance RMSD with respect to the velocities of tunes (the derivative of the f0 trajectories). This data was found to provide a weaker fit to perceptual responses and neural net classification (described below), and is therefore not reported here. However, the comparison can be found in the supplementary material on the open access repository, which includes a version of Figure 8 and Figure 14 from the paper, comparing distance based on f0 to distance based on f0 velocity. [^]
- Kaland (2021) presents another clustering methodology, which uses hierarchical agglomerative clustering for time-series f0 measures. Hierarchical clustering differs from k-means clustering in that it operates without reference to centroids, making the operation of building clusters mathematically different. Kaland (2021) also differs from the present approach in that the evaluative component of the method (i.e., determining the “best” clustering solution) is based on information cost. Nevertheless, we find that the grouping of the tunes into clusters with k-means as compared to the method from Kaland (2021) is quite similar. The online repository contains a comparison of the clustering partitions of the data with both methods, and the full dendrogram for our data, produced using the program in Kaland (2021). [^]
- The Calinski-Harabasz criterion is defined in terms of the ratio of between-cluster variance (distance between cluster centroids) to within-cluster variance (distance between an observation and the centroid of the cluster it is assigned to), also considering the number of observations and number of clusters. The optimum clustering solution is identified by a peak in the CH criterion calculated over an increasing number of clusters and corresponds to a solution with clusters that are dense and well-separated. [^]
- Input representations that were tested varied in the use of (1) time-normalized vs. raw-time measurements; (2) f0 estimates in speaker-centered Hz or ERB units, or autocorrelograms (vectors of correlations between a frame of the signal with itself at all possible lags); (3) f0 estimates at each sample x, the difference between x and the following sample (dx), or both (x & dx); and (4) the whole utterance, just the preamble, or just the nuclear word. See Figure A1 in the Appendix. [^]
- We also examined the effect of model gender within participant gender, finding that for both male and female participants, there was a credibly lower accuracy for the female model speaker, though the effect size is larger for male participants (the estimates can be found with the model on the open access repository). [^]
- We carried out several additional clustering analyses, which used registered contours. In these analyses, each trajectory was registered to syllable boundaries in the nuclear word, or to analogues of the locations of the turning points in the model stimuli. These registered analyses produced essentially the same result as the unregistered one here, and can be found in the supplementary materials in the online open access repository. [^]
- 29 out of 30 participants have a High-Rising cluster that groups HHH and HHL together. Out of these, 27 participants have a single High-Rising cluster, and two participants split the High-Rising tunes between two clusters. [^]
- We also attempted to record naturally produced stimuli directly from four phonetically trained intonation researchers in JC’s lab. Despite seeing visual images of pitch tracks for each tune and hearing recorded examples from the online ToBI training materials during the recording process, this effort was ultimately not successful as no individual succeeded in producing eight distinct tunes, based on f0 measures and auditory impression. There were also individual differences among these speakers in the tunes that were successfully distinguished and those that were not, especially for the tunes that were not reliably distinguished in our imitation data. A further concern about recording stimuli from phonetically trained intonation researchers is that f0 distinctions intentionally produced for this purpose may be (unintentionally) exaggerated or forced. [^]
- Results from our neural net (NN) classification analysis of imitated productions suggest that the preamble region may be very weakly informative about the nuclear tune category. Although NNs trained on entire utterances (preamble + nuclear region) did not yield higher overall accuracy compared those trained only on the nuclear region, NNs trained only on the prenuclear region were able to classify the nuclear tune (not included in the input) with accuracy of 12–18%, slightly above chance accuracy of 12.5% (variation in this range based on how the f0 input was coded, see Figure A1 in the appendix). For the NN trained and tested on full sentences, scalographic analysis comparing NN accuracy for analysis windows that differ in size and center location shows similar results. Expanding the analysis window to include a small amount of information from the preamble does contribute to classification accuracy for some tunes, but among all tested windows the most informative is located at about halfway through the nuclear region and spans only material in the nuclear region. From these analyses we conclude that the preamble of imitated f0 trajectories contained at best a very small amount of information about the category of the upcoming nuclear tune. [^]
Acknowledgements
The authors thank Lisa Cox for contributions to stimuli creation, and Chun Chan for technical support. We are grateful for valuable feedback on this work from the reviewers and from members of the Prosody & Speech Dynamics Lab and Phonatics Discussion Group at Northwestern University, and from audiences at these conferences: Midcontinental Phonetics and Phonology 2021, Tone and Intonation 2021, Laboratory Phonology 2022, and Speech Prosody 2022. This project was supported by NSF BCS-1944773 (Cole, PI).
Competing interests
The authors have no competing interests to declare.
References
Arvaniti, A., & Garding, G. (2007). Dialectal variation in the rising accents of American English. In J. Cole & J. I. Hualde (Eds.), Papers in laboratory phonology, 9, 547–576, Berlin: Walter de Gruyter.
Barnes, J., Brugos, A., Veilleux, N., & Shattuck-Hufnagel, S. (2021). On (and off) ramps in intonational phonology: Rises, falls, and the Tonal Center of Gravity. Journal of Phonetics, 85, 101020. DOI: http://doi.org/10.1016/j.wocn.2020.101020
Barnes, J., Veilleux, N., Brugos, A., & Shattuck-Hufnagel, S. (2012). Tonal Center of Gravity: A global approach to tonal implementation in a level-based intonational phonology. Laboratory Phonology, 3(2), 337–383. DOI: http://doi.org/10.1515/lp-2012-0017
Boersma, P., & Weenink, D. (2019). Praat: doing phonetics by computer [Computer program]. Version 6.1., retrieved from http://www.praat.org/
Bolinger, D. (1986). Intonation and its parts: Melody in spoken English. Stanford University Press. DOI: http://doi.org/10.1515/9781503622906
Braun, B., Kochanski, G., Grabe, E., & Rosner, B. S. (2006). Evidence for attractors in English intonation. The Journal of the Acoustical Society of America, 119(6), 4006–4015. DOI: http://doi.org/10.1121/1.2195267
Bürkner, P. (2018). Advanced Bayesian Multilevel Modeling with the R Package brms. The R Journal, 10(1), 395–411. DOI: http://doi.org/10.32614/RJ-2018-017
Burdin, R. S., & Tyler, J. (2018). Rises inform, and plateaus remind: Exploring the epistemic meanings of “list intonation” in American English. Journal of Pragmatics, 136, 97–114. DOI: http://doi.org/10.1016/j.pragma.2018.08.013
Caliński, T., & Harabasz, J. (1974). A dendrite method for cluster analysis. Communications in Statistics-theory and Methods, 3(1), 1–27. DOI: http://doi.org/10.1080/03610927408827101
Cole, J., & Shattuck-Hufnagel, S. (2011). The phonology and phonetics of perceived prosody: What do listeners imitate? Proceedings of Interspeech 2011, 969–972. International Speech Communication Association. DOI: http://doi.org/10.21437/Interspeech.2011-395
Cole, J., Tilsen, S., & Steffman, J. (2022). Shape matters: Machine classification and listeners’ perceptual discrimination of American English intonational tunes. Proceedings of Speech Prosody 2022, 297–301. International Speech Communication Association. DOI: http://doi.org/10.21437/SpeechProsody.2022-61
Chodroff, E., & Cole, J. (2019). Testing the distinctiveness of intonational tunes: Evidence from imitative productions in American English. In Proceedings of Interspeech 2019, 1966–1970. International Speech Communication Association. DOI: http://doi.org/10.21437/Interspeech.2019-2684
de Marneffe, M. C., & Tonhauser, J. (2019). Inferring meaning from indirect answers to polar questions: The contribution of the rise-fall-rise contour. In Questions in discourse (pp. 132–163). Brill. DOI: http://doi.org/10.1163/9789004378322_006
Dilley, L. C. (2010). Pitch range variation in English tonal contrasts: Continuous or categorical? Phonetica, 67(1–2), 63–81. DOI: http://doi.org/10.1159/000319379
Dilley, L. C., & Heffner, C. C. (2013). The role of f0 alignment in distinguishing intonation categories: evidence from American English. Journal of Speech Sciences, 3(1), 3–67. DOI: http://doi.org/10.20396/joss.v3i1.15039
Genolini, C., Alacoque, X., Sentenac, M., & Arnaud, C. (2015). kml and kml3d: R Packages to Cluster Longitudinal Data. Journal of Statistical Software, 65(4), 1–34. DOI: http://doi.org/10.18637/jss.v065.i04
Grabe, E., Post, B., Nolan, F., & Farrar, K. (2000). Pitch accent realization in four varieties of British English. Journal of Phonetics, 28(2), 161–185. DOI: http://doi.org/10.1006/jpho.2000.0111
Grice, M., Ladd, D., & Arvaniti, A. (2000). On the place of phrase accents in intonational phonology. Phonology, 17(2), 143–185. DOI: http://doi.org/10.1017/S0952675700003924
Gussenhoven, C. (2006). Experimental approaches to establishing discreteness of intonational contrasts. Methods in empirical prosody research, 321–334. DOI: http://doi.org/10.1515/9783110914641.321
Hermes, D. J. (1998). Measuring the perceptual similarity of pitch contours. Journal of Speech, Language, and Hearing Research, 41(1), 73–82. DOI: http://doi.org/10.1044/jslhr.4101.73
Hirschberg, J. (2004). Pragmatics and intonation. The Handbook of Pragmatics, 515–537. DOI: http://doi.org/10.1002/9780470756959.ch23
Jeong, S. (2018). Intonation and sentence type conventions: Two types of rising declaratives. Journal of Semantics, 35(2), 305–356. DOI: http://doi.org/10.1093/semant/ffy001
Kaland, C. (2021). Contour clustering: A field-data-driven approach for documenting and analysing prototypical f0 contours. Journal of the International Phonetic Association, 1–30. DOI: http://doi.org/10.1017/S0025100321000049
Kawahara, H., Cheveigné, A. D., Banno, H., Takahashi, T., & Irino, T. (2005). Nearly defect-free f0 trajectory extraction for expressive speech modifications based on STRAIGHT. In Ninth European Conference on Speech Communication and Technology. DOI: http://doi.org/10.21437/Interspeech.2005-335
Kingma, D. P., & Ba, J. (2014). Adam: A method for stochastic optimization. arXiv preprint https://arxiv.org/abs/1412.6980.
Ladd, D. R. Intonational phonology. Cambridge University Press, 2008. DOI: http://doi.org/10.1017/CBO9780511808814
Makowski, D., Ben-Shachar, M., & Lüdecke, D. (2019). bayestestR: Describing Effects and their Uncertainty, Existence and Significance within the Bayesian Framework. Journal of Open Source Software, 4(40), 1541. DOI: http://doi.org/10.21105/joss.01541
McAuliffe, M., Socolof, M., Mihuc, S., Wagner, M., & Sonderegger, M. (2017). Montreal Forced Aligner: Trainable Text-Speech Alignment Using Kaldi. In Proceedings of Interspeech 2017, 498–502. International Speech Communication Association. DOI: http://doi.org/10.21437/Interspeech.2017-1386
Nilsenová, M. (2006). Rises and falls. studies in the semantics and pragmatics of intonation. University of Amsterdam.
Penney, J., Cox, F., & Szakay, A. (2020). Glottalisation, coda voicing, and phrase position in Australian English. The Journal of the Acoustical Society of America, 148(5), 3232–3245. DOI: http://doi.org/10.1121/10.0002488
Pierrehumbert, J. (1980). The phonology and phonetics of English intonation [PhD thesis]. Massachusetts Institute of Technology.
Pierrehumbert, J. B., & Steele, S. A. (1989). Categories of tonal alignment in English. Phonetica, 46(4), 181–196. DOI: http://doi.org/10.1159/000261842
Prieto, P. (2015). Intonational meaning. Wiley Interdisciplinary Reviews: Cognitive Science, 6(4), 371–381. DOI: http://doi.org/10.1002/wcs.1352
Roessig, S., Mücke, D., & Grice, M. (2019). The dynamics of intonation: Categorical and continuous variation in an attractor-based model. PLoS ONE, 14(5). DOI: http://doi.org/10.1371/journal.pone.0216859
Roettger, T. B., & Grice, M. (2019). The tune drives the text. Language Dynamics and Change, 9(2), 265–298. DOI: http://doi.org/10.1163/22105832-00902006
Rudin, D. (2022). Intonational commitments. Journal of Semantics, 39(2), 339–383. DOI: http://doi.org/10.1093/jos/ffac002
Shue, Y.-L., Keating, P., Vicenik, C., & Yu, K. (2011). VoiceSauce: A program for voice analysis. In Proceedings of ICPhS XVII, 1846–1849.
Sóskuthy, M. (2021). Evaluating generalised additive mixed modelling strategies for dynamic speech analysis. Journal of Phonetics, 84, 101017. DOI: http://doi.org/10.1016/j.wocn.2020.101017
Steffman, J., & Cole, J. (2022). An automated method for detecting F0 measurement jumps based on sample-to-sample differences. JASA Express Letters, 2(11), 115201. DOI: http://doi.org/10.1121/10.0015045
Tilsen, S., Burgess, D., & Lantz, E. (2013). Imitation of intonational gestures: a preliminary report. Cornell Working Papers in Phonetics and Phonology, 1–17. https://zenodo.org/record/3726928#.YxDaCtPMKUk
van Rij, J., Wieling, M., Baayen, R., & van Rijn, H. (2016). Itsadug: Interpreting time series and autocorrelated data using GAMMs [R package]. https://research.rug.nl/en/publications/itsadug-interpreting-time-series-and-autocorrelated-data-using-ga
Vasishth, S., Nicenboim, B., Beckman, M. E., Li, F., & Kong, E. J. (2018). Bayesian data analysis in the phonetic sciences: A tutorial introduction. Journal of phonetics, 71, 147–161. DOI: http://doi.org/10.1016/j.wocn.2018.07.008
Veilleux, N., Shattuck-Hufnagel, S., & Brugos, A. 6.911 Transcribing Prosodic Structure of Spoken Utterances with ToBI. January IAP 2006. Massachusetts Institute of Technology: MIT OpenCourseWare, https://ocw.mit.edu. License: Creative Commons BY-NC-SA.
Westera, M., Goodhue, D., Gussenhoven, C., & Chen, A. (2020). Meanings of tones and tunes. The Oxford Handbook of Language Prosody, 443–453. DOI: http://doi.org/10.1093/oxfordhb/9780198832232.013.29
Wood, S. N. (2017). Generalized additive models: An introduction with R. Chapman and Hall/CRC. DOI: http://doi.org/10.1201/9781420010404